Непримитивность рекурсивности функции Аккермана

Введение

Функция Аккермана - важная функция в теоретической информатике, она всюду определена и не является примитивно рекурсивной.

Функция Аккермана ввиду своей рекурсивности находит широкое применение в тестах производительности, она сохраняет промежуточные результаты выполнения функций для предотвращения повторных вычислений, что в целом оптимизирует и ускоряет работу программы.

Функция Аккермана - это непримитивно рекурсивная функция вида:

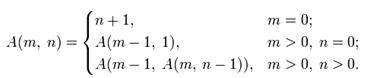
Функция принимает на вход два неотрицательных числа m и n, а на выходе дает натуральное число.

Проведем анализ алгоритма:

1. Если m = 0, то А(0, n) = n + 1.

2. Если m = 1, то А(1, n) = А(0, А(1, n – 1)) = А(1, n – 1) + 1 = А(1, n – 2) + 2 = … = А(1, 0) + n = А(0, 1) + n = 2 + n.

3. Если m = 2, то А(2, n) = А(1, A(2, n – 1)) = А(2, n – 1) + 2 = А(2, n – 2) + 4 = … = А(2, 0) + 2n  = А(1, 1) + 2n  = 2 + 1 + 2n  =  2n + 3.

4. Если m = 3, то А(3, n) = А(2, A(3, n – 1)) = 2 * А(3, n – 1) + 3 = 2 * (2 * А(3, n – 2) + 3) + 3 = 4 * А(3, n – 2) + 3*2 + 3 = 8 * А(3, n – 3) + 3*4 + 3*2 + 3 = … = 2n * А(3, 0) + 3*2n–1 + … + 3*4 + 3*2 + 3 = 2n * А(2, 1) + 3*(2n – 1) = 2n * (2*1 + 3) + 3*2n – 3 = 2n+3 – 3.

Таким образом, мы получаем, что:

A(0, n) = n + 1,

A(1, n) = n + 2,

A(2, n) = 2n + 3,

A(3, n) = 2ⁿ⁺³ – 3                                                                                                                  (1)

Мы получили формулы для вычисления функции Аккермана для m≤3. Из их вывода, так же, как и из определения, можно увидеть, что функция Аккермана - рекурсивная функция.

К числу базовых примитивно рекурсивных функций относятся функции следующих трёх видов:

· Нулевая функция — функция без аргументов, всегда возвращающая 0.

· Функция следования S одного переменного, сопоставляющая любому натуральному числу x непосредственно следующее за ним натуральное число x + 1.

· Функции, где , от n переменных, сопоставляющие любому упорядоченному набору  натуральных чисел число  из этого набора.

Из (1) видно, что при m = 3, функция Аккермана растет уже гораздо быстрее, чем при m = 2.

Таблица 1.

Значения функции Аккермана при m = 2 и при m = 3

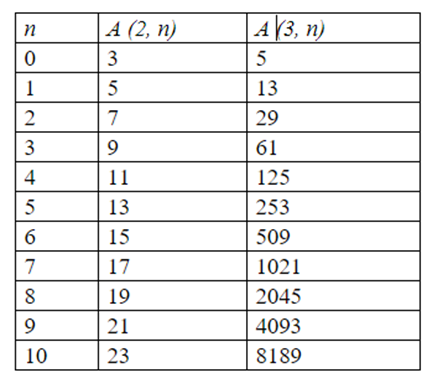
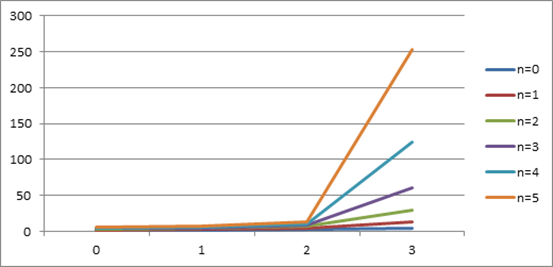
Рисунок 1. функция Аккермана при фиксированных n

Из графика 1 видно, что при фиксированном m и при увеличении n скорость возрастания функции Аккермана резко увеличивается.

То же самое поведение функции наблюдается также при фиксированном n и при увеличении m.

Подобная тенденция к резкому увеличению скорости нехарактерна для примитивно рекурсивных функций, откуда можно сделать вывод, что функция Аккермана не является примитивно рекурсивной.

Докажем, что функция Аккермана не является примитивно рекурсивной. 

Прежде всего, нужно отметить, что для этого мы ограничиваем функцию g:

Для унарных функций неравенство будет выполняться для каждого входного значения, так что  во всех точках.

Доказательство:

Во-первых, докажем, что состав примитивно-рекурсивных функций не может расти с большей скоростью, чем функция Аккермана.

Допустим , где f, g, h –примитивно рекурсивные функции.

так, что , где  являются первыми параметрами функции Аккермана. Затем допустим, что , тогда мы должны показать, что:

Распишем композицию функции Аккермана:

x раз

Рассмотрим два выражения, которые помогут в доказательстве. Можно заметить, что:

                                                                                                                         (2)

                                                                                                                   (3)

Мы можем показать, что (2) следует из того, что . Теперь из выражения (1) мы видим, что при значениях х=3 и m=1 значение  = 5. Так как при увеличении m будет расти значение композиции функции Аккермана, то выражение (2) выполняется.

Рассмотрим выражение (3) и распишем функцию Аккермана в виде:

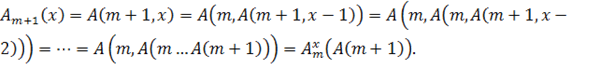
Отсюда видно, что выражение (3) - доказано, так как простой случай, когда число композиций Аккермана равно 0, то есть 

Вспоминаем наши начальные неравенства:

,

где   – примитивно рекурсивная функция.

Теперь можно заметить, что:

 ,

но

Можно заметить: . Отсюда видно, что существует значение функции Аккермана, которое строго больше композиции любых двух примитивно рекурсивных функций, имеющих одинаковые входные значения, и состав примитивно-рекурсивных функций не может расти с большей скоростью, чем функция Аккермана.

Во- вторых, докажем, что рекурсивная конкатенация примитивно рекурсивных функций не может увеличиваться с большей скоростью, чем функция Аккермана.

Для этого предположим, что существует функция f(x) определяемая рекуррентными уравнениями:

f(0) = c

f(n + 1) = g(n, f(n)).

Тогда, поскольку функция  является примитивно рекурсивной, мы знаем, что существует функция Аккермана , которая больше, чем функция , и мы можем показать, что выражение  справедливо для некоторого m > 0.

Воспользуемся методом математической индукции:

Нам известно, что  является постоянной функцией, являющейся примитивно-рекурсивной унарной проекционной функцией, поэтому по более ранним наблюдениям существует функция Аккермана,  > .

Предположим, что наблюдение выполняется для всех случаев .

Пусть , а 

Тогда:

так как функция g возрастает. По предположению индукции мы знаем:

Отсюда делаем подстановку и тогда нашим выбором для  получаем:

Отсюда мы знаем по определению функции Аккермана и подстановки, что:

Теперь мы можем сказать, что выражение  справедливо, откуда следует, что функция Аккермана не является примитивно рекурсивной, так как она возрастает быстрее всех примитивно рекурсивных функций.

Вывод

В ходе работы было проведено доказательство того, что функция Аккермана не является примитивно рекурсивной.