Использование методов линейного программирования для решения оптимальных задач на предприятии ООО «Бигэ»
Конференция: LXXXIX Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Физико-математические науки

LXXXIX Студенческая международная научно-практическая конференция «Молодежный научный форум»
Использование методов линейного программирования для решения оптимальных задач на предприятии ООО «Бигэ»
Аннотация. В данной работе изученные теоретические положения были применены на конкретном предприятии – ООО «Бигэ» в построении ЭММ по определению оптимального ассортимента продукции – был рассчитан такой план производства, при котором наблюдалась бы максимальная прибыль при располагаемом запасе ресурсов и трудоемкости технологического процесса.
Ключевые слова: экономико-математическая модель (ЭММ), симплекс метод.
Часто эксперимент с математической моделью может заменить реальный эксперимент, который невозможен по тем или иным причинам. Все это и дает весомую актуальность применению задач линейного программирования в современных экономических условиях.
Пользуясь статистическими данными деятельности предприятия, составим экономико-математическую модель задачи по определению оптимального ассортимента продукции.
Таблица 1.
Производство продукции
|
Наименование изделия |
Ед.изм. в кг |
Цена, руб. |
Усл. обознач. |
|
ARCTIC грунтовка бетон-контакт |
21 |
105*21=2205 |
|
|
ARCTIC акриловая моющаяся |
21 |
170*21=3570 |
|
|
DECO краска фасад |
21 |
93*21=1953 |
|
|
ARCTIC краска огнезащитная по дереву |
21 |
350*21=7350 |
|
|
ARCTIC эмаль матовый |
21 |
225*21=4725 |
|
Для производства пяти видов продукции (в таблице) ООО «Бигэ» использует десять составов. Нормы затрат ресурсов на одно изделие каждого вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:
Таблица 2.
Нормы затрат ресурсов на одно изделие каждого вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида
|
Ресурсы |
Нормы затрат составов |
Общее количество составов,кг |
||||
|
|
|
|
|
|
||
|
1 вид (состав,кг) |
7 |
5 |
6 |
8 |
10 |
300 |
|
2 вид (состав,кг) |
0 |
2 |
1 |
0 |
1 |
60 |
|
3 вида (состав,кг) |
0 |
0 |
0 |
0 |
5 |
90 |
|
4 вида (состав,кг) |
3 |
3 |
2 |
0 |
2 |
89 |
|
5 вида (состав,кг) |
9 |
8 |
5 |
6 |
3 |
273 |
|
6 вида (состав,кг) |
2 |
0 |
0 |
0 |
0 |
58 |
|
7 вида (состав,кг) |
0 |
1 |
1 |
0 |
0 |
42 |
|
8 вида (состав,кг) |
0 |
0 |
4 |
1 |
0 |
82 |
|
9 вида (состав,кг) |
0 |
2 |
2 |
1 |
0 |
64 |
|
10 вида (состав,кг) |
0 |
0 |
0 |
5 |
0 |
151 |
|
Прибыль от реализации, тыс. руб. |
2205 |
3570 |
1953 |
7350 |
4725 |
|
Определим, сколько кг каждого изделия следует изготавливать предприятию, чтобы прибыль от их реализации была максимальной.
Решение:
Обозначим изделие каждого вида соответственно
![]() . Тогда на изготовление всей продукции уйдет
. Тогда на изготовление всей продукции уйдет
(7x1+5x2+6x3+8x4+10x5) кг составы I вида,
(2x2+x3+x5 ) кг составы II вида,
(5x5) кг составы III вида,
(3x1+3x2+2x3+2x5 ) кг составы IV вида,
(9x1+8x2+5x3+6x4+3x5 ) кг составы V вида,
(2x1) кг составы VI вида .
(x2+x3) кг составы VII вида,
(4x3+x4) кг составы VIII вида,
(2x2+2x3+x4) кг составы IX вида .
(5x4) кг составы X вида .
Так как запасы этих ресурсов не превышают 300кг, 60кг, 90кг, 89кг, 273кг, 58кг, 42кг, 82кг, 64кг, 151кг соответственно, то
7x1+5x2+6x3+8x4+10x5≤300
2x2+x3+x5≤60
5x5≤90
3x1+3x2+2x3+2x5≤89
9x1+8x2+5x3+6x4+3x5≤273
2x1≤58
x2+x3≤42
4x3+x4≤82
2x2+2x3+x4≤64
5x4≤151
Итак, система ограничений имеет вид:
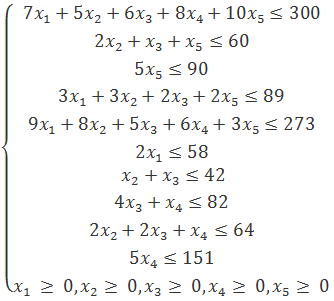
А прибыль будет выражена функцией
F(X) = 2205x1+3570x2+1953x3+7350x4+4725x5
Нахождения решения задачи симплекс методом.
Окончательный вариант симплекс-таблицы:
|
Базис |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
x11 |
x12 |
x13 |
x14 |
x15 |
|
x5 |
41/325 |
11/65 |
0 |
23/65 |
0 |
1 |
8/65 |
0 |
0 |
0 |
-1/13 |
0 |
0 |
0 |
0 |
-34/325 |
|
x7 |
12031/325 |
-149/65 |
0 |
-22/65 |
0 |
0 |
-2/65 |
1 |
0 |
0 |
-3/13 |
0 |
0 |
0 |
0 |
106/325 |
|
x8 |
5809/65 |
-11/13 |
0 |
-23/13 |
0 |
0 |
-8/13 |
0 |
1 |
0 |
5/13 |
0 |
0 |
0 |
0 |
34/65 |
|
x9 |
17701/325 |
-34/65 |
0 |
-12/65 |
0 |
0 |
-7/65 |
0 |
0 |
1 |
-4/13 |
0 |
0 |
0 |
0 |
176/325 |
|
x2 |
3714/325 |
69/65 |
1 |
32/65 |
0 |
0 |
-3/65 |
0 |
0 |
0 |
2/13 |
0 |
0 |
0 |
0 |
-36/325 |
|
x11 |
58 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
x12 |
9936/325 |
-69/65 |
0 |
33/65 |
0 |
0 |
3/65 |
0 |
0 |
0 |
-2/13 |
0 |
1 |
0 |
0 |
36/325 |
|
x13 |
259/5 |
0 |
0 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
-1/5 |
|
x14 |
3557/325 |
-138/65 |
0 |
66/65 |
0 |
0 |
6/65 |
0 |
0 |
0 |
-4/13 |
0 |
0 |
0 |
1 |
7/325 |
|
x4 |
151/5 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1/5 |
|
F(X4) |
17118591/65 |
30996/13 |
0 |
19194/13 |
0 |
0 |
5418/13 |
0 |
0 |
0 |
2415/13 |
0 |
0 |
0 |
0 |
37716/65 |
Итак, чтобы получить максимальную прибыль 263363 рублей при имеющихся запасах сырья и существующей трудоемкости получаемой продукции, предприятию следует производить 0 единиц товара вида ![]() , 11– вида
, 11– вида ![]() , 0 – вида
, 0 – вида ![]() , 30,2- вида
, 30,2- вида ![]() и 0,13 – вида
и 0,13 – вида ![]() .
.





