Обобщение классов Поста на случай трехзначной логики

Задачи

Обобщить классы Поста на случай трехзначной логики;

Доказать их замкнутость.

Функции двузначной и трехзначной логики

В курсе дискретной математики рассматриваются булевы функции, то есть функции многих переменных, каждый аргумент которых и сами функции могут принимать лишь два значения: 0 и 1. Множество булевых функции обозначается .

Функции двузначной логики  – это отображения вида

Функции многих переменных, каждый аргумент которых и сами функции могут принимать три значения: 0, 1 и 2. Полученные функции обозначаются .

Получилось, что функции трехзначной логики  – это отображения вида

Предполные классы

Замыканием множества булевых функций u называется множество всех суперпозиций функций класса , которое обозначается . Класс  называется функционально полным, если .

Предполный класс в теории булевых функций – это замкнутый класс булевых функций, обладающий следующим свойством: замыкание объединения этого класса с любой булевой функцией, не принадлежащей ему, порождает весь класс .

В классе  есть 5 предполных класса, называемых классами Поста:

1. Класс функций, сохраняющий константу 0:

2. Класс функций, сохраняющий константу 1:

3. Класс линейных функций:

4. Класс самодвойственных функций:

Говорят, что набор  предшествует набору  и пишут , если где 

5. Класс монотонных функций:

При переходе от двузначного случая к трехзначному наблюдается увеличение количества предполных классов. Таким образом, в   есть 18 предполных классов:

1. Класс функций, сохраняющий константу 0:

2. Класс функций, сохраняющий константу 1:

3. Класс функций, сохраняющий константу 2:

Для следующих трех классов, сохраняющих множество, доказано, что каждый из них является позитивным замыканием множества всех своих одноместных функций:

4. Класс функций, сохраняющий множество {0,1}:

5. Класс функций, сохраняющий множество {0,2}:

6. Класс функций, сохраняющий множество {1,2}:

7. Класс самодвойственных функций S:

Отрицание введено как отрицание Поста:  То есть этот класс является классом, сохраняющим отношение 

8. Класс линейных функций:

9. Класс монотонных функций M_0 относительно порядка :

10. Класс монотонных функций M_1 относительно порядка :

11. Класс монотонных функций M_2 относительно порядка 

12.  Класс  сохранения разбиения 

13. Класс  сохранения разбиения 

14. Класс  сохранения разбиения 

15. Центральный предполный класс , сохраняющий отношение 

16. Центральный предполный класс , сохраняющий отношение 

17. Центральный предполный класс , сохраняющий отношение 

18. Предполный класс Слупецкого  такой, что все трехзначные функции имеют либо не более одной существенной переменной, либо принимают не более двух значений.

В таблице 1 указаны строки принадлежности всех трехзначных функций, имеющих не более одной существенной переменной. Каждой функции поставим в соответствие строку принадлежности: «+», если  принадлежит соответствующему предполному классу, и «-», если  не принадлежит соответствующему предполному классу.

Таблица 1

Доказательство замкнутости некоторых предполных классов.

- замкнутый класс.

Доказательство. Пусть дана произвольная систему функций  из  и функция . Среди переменных функций  могут встречаться и одинаковые, поэтому в качестве переменных функции  берутся все различные из них. Тогда  Следовательно, функция  также сохраняет ноль. Рассмотрен только частный случай (без переменных в качестве аргументов). Однако, поскольку тождественная функция сохраняет ноль, подстановка простых переменных эквивалентна подстановке тождественной функции, что и требовалось доказать.

Аналогично доказывается замкнутость классов 

S - замкнутый класс.

Доказательство. Пусть  и .

Тогда из принципа двойственности следует, что

                           .

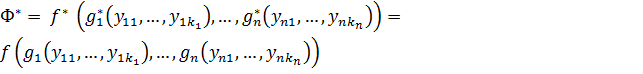Получается, что  и , что и требовалось доказать.

L - замкнутый класс.

Доказательство. Поскольку тождественная функция – линейная, достаточно рассмотреть только случай подстановки в формулы функций: пусть  и  Достаточно доказать, что . Действительно, если не учитывать слагаемых с коэффициентами , то всякую линейную функцию можно представить в виде . Если теперь вместо каждого  подставить линейное выражение, то получится снова линейное выражение или константа 0, 1 или 2.

 - замкнутый класс.

Доказательство. Поскольку тождественная функция монотонна, достаточно проверить лишь случай суперпозиции функций. Пусть  и . Пусть даны произвольные наборы  такие, что  Тогда  Следовательно  и , то есть . Пусть . Тогда по определению и, в силу монотонности функции  имеем  Но ,

, откуда , следовательно , что и требовалось доказать.

Аналогично доказывается замкнутость классов  и .

Заключение

В ходе выполнения работы были обобщены классы Поста на случай трехзначной логики. Также была доказана замкнутость некоторых из них.