Разработка e-learning курса «Математическая логика» в интеллектуальной системе обучения математике Math-Bridge

Практически все сферы жизни современного человека существенно изменились под влиянием компьютерных и информационных технологий. Сфера образования не стала исключением, поскольку информатизация образовательного процесса в РФ – это один из важнейших механизмов, затрагивающий основные направления модернизации всей образовательной системы. Вследствие этого наряду с традиционными формами образования появилась новая форма обучения – дистанционная.

Обзор программных средств для создания электронных учебников.

В качестве основной платформы, для эффективной организации учебного процесса и обеспечения постоянного доступа студентов и преподавателей к учебным материалам, мы решили использовать систему дистанционного обучения Math-Bridge, в силу своей доступности, легкости в изучении и использовании.

MathBridge – это специальная система для обучения математике немецкого института по искусственному интеллекту, построенная совершенно на других принципах, чем остальные системы. Она поддерживает богатый образовательный опыт: включает большой объем учебного материала с достаточно подробной наглядной компьютерной иллюстрацией изучаемых математических моделей и методов, контрольные задания, предполагающие не только выбор одного из заданных ответов, а формирование обучающимся последовательности шагов, ведущих к решению.

Исследования эффективности разработанной в DFKI e-learning системы проводились в технических ВУЗах Франции, Германии и Финляндии. В Российской Федерации система Math-Bridge внедряется в рамках Европейского образовательного проекта TEMPUS-MetaMath, участником которого является Казанский национальный технический университет им. А.Н. Туполева-КАИ (КНИТУ-КАИ).

Процесс разработки. Создание курса «Математическая логика»

Прежде чем создавать новый курс, познакомимся с интерфейсом программы на существующем сайте, размещенном по адресу http://mathbridge.kai.ru/mathbridge/#.

Ее интерфейс состоит из нескольких виджетов обеспечивающих доступ к различным функциям системы: обычные и адаптивные курсы, вопросники, тесты и экзамены, закладки (Рис.1). Далее заходим на курс в качестве зарегистрированного пользователя.

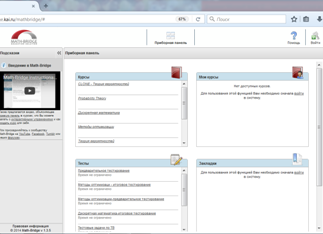
Рисунок 1. Главная страница сайта

После входа, в верхней части страницы выбираем меню «Авторинг» (Рис.2). Здесь вы можете создавать и управлять объектами обучения, а также публиковать объекты, чтобы сделать их доступными для студентов.

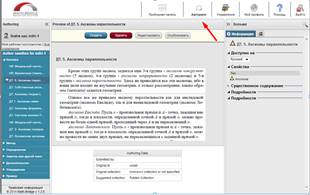
Рисунок 2. Переключение в режим авторинга

Создание нового объекта

Для создания нового объекта нажимаем кнопку «Создать» на панели команд.

Рисунок 3. Панель инструментов

После того, как откроется всплывающее меню, выбираем тип создаваемого учебного объекта. Между собой учебные объекты в системе Math-Bridge подразделяются на три вида: динамические, статические и структурные объекты обучения (Рис.4.). Пусть в нашем случае это будет «Аксиома».

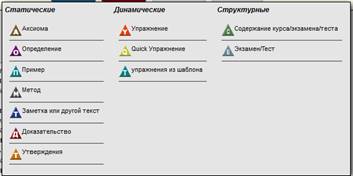
Рисунок 4. Меню для создания учебного объекта

В открывшемся редакторе слева сверху пишем название лекции, а слева выбираем тип Publish Collection, чтоб этот объект можно было использовать любым другим автором для создания курса или экзамена (Рис. 5). Далее нажимаем на иконку «Добавить изображение» в редакторе. Появиться окно (Рис. 6.), в котором надо нажать на кнопку Обзор и найти ранее сохраненное изображение на компьютере, затем нажимаем кнопку Загрузить.

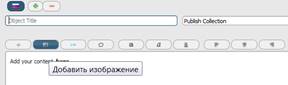
Рисунок 5. Область редактирования

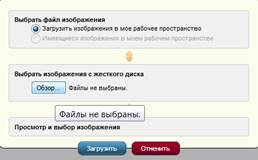
Рисунок 6. Окно загрузки изображения

После загрузки сохраняем объект.

Использование возможностей Math-Bridge для создания упражнений

Не менее важными представляются возможности системы в области создания упражнений – динамических учебных объектов, напрямую взаимодействующих с пользователем.

Для создания упражнения нажимаем кнопку «Создать» на панели команд. Выбираем из динамических объектов пункт «Упражнение из шаблона». В открывшемся окне «Шаблоны» выбираем стандартный шаблон – “One Interaction-Simple Exercise”. Далее нажимаем «Ок».

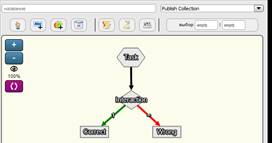
Рисунок 7. Страница редактирования

В открывшемся редакторе слева сверху, где поле для ввода пишем название лекции, а слева выбираем тип Publish Collection.

Граф упражнения отображает содержимое в виде последовательности шагов и их соединений. Основная задача при использовании шаблонов ввести информацию внутрь фигур и связей. Нажатием на кнопку «Выбрать» , активизируем элементы шаблона графа, теперь можно заходить внутрь фигур и связей графа простым щелчком Мыши. Фигура под названием “Task” – означает начало упражнения, то есть Задание. В поле ввода имени вводится название упражнения, в поле ввода задачи вводится условие задачи(Рис.8). Фигура под названием “Interaction” – означает условие. Это поле ввода ответа и “Checkbox”.

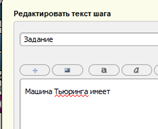
Рисунок 8. Поле ввода задачи

С помощью кнопки «Поле выбора» добавляем несколько ответов.

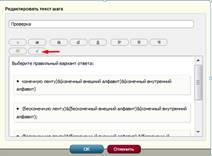
Рисунок 9. Поле ввода ответа

После заполнения всех полей переходим к редактированию шагов графа. В поле «Условие» на верный ответ ставим галочку. А в поле «Диагностика» щелчком мыши выбираем «зеленую связь», т.е. оценку – «1» (Рис.10).

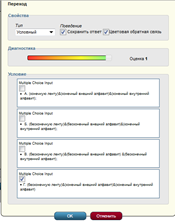
Рисунок 10. Настройка правильного ответа

Затем переходим к следующему шагу, к неправильному ответу. Здесь уже в поле «Диагностика» щелчком мыши выбираем не зеленую, а «красную связь», т.е. оценку – «0». И в поле «Свойства» указываем Тип – «По умолчанию» (Рис.11).

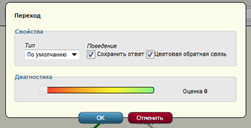
Рисунок 11. Настройка неправильного ответа

После ввода всех данных во все элементы графа, упражнение сохраняем командой «Сохранить», а затем запускаем на выполнение командой “Run”.

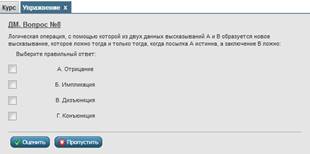
Рисунок 12. Результат запуска созданного динамического объекта

Сборка и опубликование курса.

Для опубликования любого учебного объекта, сохраняем объект и нажимаем на кнопку «опубликовать» на панели управления объектами. После этого объект появится в общем рабочем пространстве и будет помещен в раздел, соответствующий его типу. Далее, перейдя в режим Управления, создаем книги для теоретического материала и тестовых заданий на экзамене, куда затем скопируем опубликованные ранее объекты. Для опубликования книги переходим в режим Приборной панели и в окне «Мои курсы» напротив созданной книги нажимаем на кнопку  – «опубликовать».

Теперь курс доступен для изучения. Курс реализован на русском языке, хотя система MathBridge позволяет представлять учебные объекты более чем на 10 языках.

ЗАКЛЮЧЕНИЕ

Таким образом, используя все доступные инструменты e-learning системы Math-Bridge возможно создать полноценный математический курс с интеллектуальной системой взаимодействия с обучаемым. Обладая высокой степенью интерактивности, разработанные курсы способны адаптироваться к потребностям и особенностям каждого обучаемого, увеличивая эффективность и глубину усвоения учебного материала.

Учебный курс представляет собой набор учебно-методических материалов, оформленных специальным образом в виде объектов сервера дистанционного обучения. Перечисленные уникальные возможности среды Math-Bridge по использованию в составе обучающих объектов делают использование данной e-learning системы незаменимым.