Двудольные графы и их применение в кодировании информации

ВВЕДЕНИЕ

Целью данной работы является изучение алгоритмов Хаффмана и Шеннона-Фано, провести их сравнительную характеристику и выявить, какой алгоритм более эффективный и оптимальный.

Для достижения данной цели были поставлены следующие задачи: изучение понятия двудольных графов, основных определений деревьев, этапов кодирования алгоритмов Хаффмана и Шеннона-Фано.

Для составления сравнительной характеристики алгоритмов будут выбраны 12 высказываний разной длины. И для каждого из них проведутся алгоритмы на разных языках. В работе алгоритмы будут сравниваться по количеству символов в сообщении, по количеству символов в коде, по времени выполнения кода и по количеству символов, составляющие сообщение.

ПОНЯТИЕ ДВУДОЛЬНОГО ГРАФА И ДЕРЕВЬЕВ

Двудольным графом (биграфом) называется граф, у которого множество вершин можно разбить на 2 части, так что каждое ребро соединяет одну вершину из одной части графа с другой вершины из другой части графа, то есть ребра между одной и той же части графа не существует.

Двудольные граф - это неориентированный граф G=(W,E), в котором множество вершин разбивается на две части U 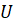 V = W, при условии, что нет таких вершин из множества U (V), которые соединены с вершинами из этого же множества U (V) Такие подмножества вершин (U и V) являются долями этого графа.

Теорема Кёнига 2 (о условии разбития множества вершин) если граф не содержит цикл нечетной длины, тогда граф является двудольным.

Немало важно, отметить тот факт, что из теоремы Кёнига 2 вытекает следующее следствие:

Любое дерево является связным двудольным графом.

Это легко доказать уже из определения дерева, ведь дерево - это связный ацикличный граф, в котором нет циклов нечетной длины, а также циклов и четной длины.

Стоит упомянуть, что в информатике дерево — это структура данных, модулирующая древовидную структуру в формате множества связанных узлов. Также одними из свойств является отсутствие ориентированности и взвешенности.

Дадим основные определения для дерева в качестве структуры данных.

Дерево T – это конечное множество узлов, в котором существует один выделенный узел t, корень дерева, а остальные узлы, разбитые на M  0 непересекающихся множеств T1,T2,…,TM, где каждое само является деревом, которое называется поддеревом узла t.

Корень дерева t – это предшественник, предок или родительский узел по отношению к остальным корням  своих поддеревьев  .

А узлы  – это преемники, потомки или дочерние узлы.

ПРИМЕНЕНИЕ ДЕРЕВИЕВ

Деревья применяются в управлении иерархией данных. Также благодаря им упрощается поиск той или иной информации. С помощью такой структуры данных осуществляется управление сортированными списками данных. В добавок, используются для оптимизации программ, синтаксического разбора арифметических выражений. Более того, их можно применять в качестве одной из технологий компоновки цифровых картинок для получения различных визуальных эффектов. Еще деревья могут служить формой принятия многоэтапного решения.

Также удобно применять структуры данных – деревья в различных алгоритмах кодирования. Одним из известных алгоритмов кодирования является алгоритм Хаффмана.

АЛГОРИТМ ХАФФМАНА

Алгоритм Хаффмана — это алгоритм оптимального префиксного кодирования алфавита. Он был разработан в 1952 году Дэвидом Хаффманом. Интересным фактов является то, что в то время он был аспирантом Массачусетского технологического института и данный алгоритм был произведен при написании Хаффманом курсовой работы.  Его алгоритм используется во многих программах сжатия данных таких как PKZIP 2 и LZH.

Алгоритм:

1. Находится вероятность появления того или иного символа в сообщении и располагается в порядке убывания.
2. Берутся два наименее вероятных символа (т.е. два последних) в алфавите и объединяются в один, а вероятность нового элемента равна сумме вероятностей объединенных символов. Это действие повторяется на каждом этапе.
3. Производится пересортировка списка по убыванию вероятностей, с сохранением информации о том, какие именно знаки объединялись на каждом этапе.

И так этот алгоритм продолжается до тех пор, пока не останется единственный элемент с вероятностью, равной 1.

Само кодирование осуществляется с помощью кодового дерева.

1. Корню дерева соответствует узел с вероятностью, равной 1.
2. Далее каждому узлу приписывается два потомка - левый и правый, с теми вероятностями, которые участвовали в образовании значения вероятности текущего узла. Так этот процесс продолжатся до достижения узлов, которые соответствовали вероятностям начальных символов.  Для ветви, например, правой, которая выходит с более высокой вероятностью, ставится в соответствие символ 1, а с меньшей – 0, например, левая ветвь.  И так спускаясь от корня к необходимому символу, можно получить код соответствующий этому символу.

АЛГОРИТМ ШЕННОНА-ФАНО

В теории кодирования существует алгоритм, похожий на алгоритм Хаффмана, однако в нем не используются деревья.

Это кодирования относится к вероятностному методу сжатия, в котором коды более частых символов заменяются на двоичные последовательности, а коды редких символов – на длинные последовательности.

Алгоритм следующий:

Список вероятностей для данного набора символов, записываем в порядке убывания. Разделяем список на 2 части, при этом сумма вероятностей каждой части должны быть примерно одинаковы. Далее все знаки одной группы кодируем нулем, другой группы единицей. Затем каждую из подгрупп разделяем на еще 2 группы по тому же принципу, и кодируем их. Так делаем до тех пор, пока не закодируем каждый знак.

СРАВНИТЕЛЬНАЯ ХАРАКТЕРИСТИКА АЛГОРИТМОВ: ШЕННОНА-ФАНО И ХАФФМАНА

Для составления сравнительной характеристики алгоритмов было выбрано 12 высказываний разной длины:

1. Математика заключает в себе не только истину, но и высочайшую красоту - красоту холодную и строгую, подобную красоте скульптуры. (-Бертран Рассел)
2. Книга природы написана на языке математики. (-Галилео Галилей)
3.  Как воздух, математика нужна, Самой отваги офицеру мало. Расчеты! Залп! И цель поражена Могучими ударами металла. И воину припомнилось на миг, Как школьником мечтал в часы ученья: О подвиге, о шквалах огневых, О яростном порыве наступленья. Но строг учитель был, И каждый раз он обрывал мальчишку грубовато: — Мечтать довольно, повтори рассказ О свойствах круга и углах квадрата. И воином любовь сохранена К учителю далекому, седому. Как воздух, математика нужна Сегодня офицеру молодому.
4. «Text 2. What is Mathematics?» из учебно-методического пособия Е.Н.Пушкина «English for Mathematicians and Information Technologies Learners» [6]
5. «Text 6. Information, Machine Words, Instructions, Addresses and Reasonable Operations» из учебно-методического пособия Е.Н.Пушкина «English for Mathematicians and Information Technologies Learners» [6]
6. Математика выявляет порядок, симметрию и определённость, а это – важнейшие виды прекрасного. (Аристотель)
7. Между духом и материей посредничает математика. (Хуго Штейнгаус)
8. Нельзя быть настоящим математиком, не будучи немного поэтом. (К. Вейерштрасс)
9. Математика
10. Химия – правая рука физики, математика – ее глаз. (М.В. Ломоносов)
11. С тех пор как за теорию относительности принялись математики, я ее уже сам больше не понимаю. (Альберт Эйнштейн)
12. Рассказ о математике «Евклид» Василия Дмитриевича Чистякова [5]

И для каждого из них проводились алгоритмы Хаффмана и Шеннона-Фано на разных языках: английском, русском, французском, итальянском, сербском, арабском, греческом, белорусском, ивритском, немецком и турецком.

Сравнение происходило по следующим параметрам: количество символов в сообщении, количество символов в коде, время выполнения кода, количество символов, составляющие таблицу кодировки и степень сжатия.

Степень сжатия вычисляется по формуле:

                                                                                                              (1)

где:

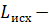 объем данных исходного сообщения (длина сообщения*8 [биты]);

 объем данных сжатого сообщения (длина сжатого сообщения *1 [биты]).

АЛГОРИТМ ХАФФМАНА

С помощью кода Хаффмана были составлены таблицы, в которых наглядно представлено выполнения данного алгоритма для каждого из высказываний. Тем самым, легко определить на каком языке осуществляется эффективное кодирование.

Для 1 строки:

Таблица 1.

Характеристики 1 строки на разных языках. Алгоритм Хаффмана

Среднее значение степени сжатия = 47%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у итальянского языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у ивритского и итальянского языков.

Для наглядного представления рассмотрим одну из самых длинных строк – 5 строку.

Для 5 строки:

Таблица 2.

Характеристики 5 строки на разных языках. Алгоритм Хаффмана

Среднее значение степени сжатия = 44%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у немецкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у французского и итальянского языков.

Для остальных строк укажим наилучшие характеристики.

Для 2 строки:

Среднее значение степени сжатия = 50%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у сербского языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у арабского языка.

Для 3 строки:

Среднее значение степени сжатия = 44%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у ивритского языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у итальянского языка.

Для 4 строки:

Среднее значение степени сжатия = 45 %. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у французского языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у итальянского языка.

Для 6 строки:

Среднее значение степени сжатия = 48%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у турецкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у французского, итальянского, арабского и ивритского языков.

Для 7 строки:

Среднее значение степени сжатия = 51%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у французского языка.  Минимальное количество символов, составляющих таблицу кодировки, у итальянского языка. Максимальная степень сжатия у итальянского языка.

Для 8 строки:

Среднее значение степени сжатия =50 %. Минимальное количество символов в сообщении у турецкого языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у арабского языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у французского языка.

Для 9 строки:

Среднее значение степени сжатия = 66%. Минимальное количество символов в сообщении у английского и немецкого языков. Минимальное количество символов в коде у английского и немецкого языков. Минимальное время выполнения кода у арабского языка.  Минимальное количество символов, составляющих таблицу кодировки, у английского, немецкого и арабского языков. Максимальная степень сжатия у арабского языка.

Для 10 строки:

Среднее значение степени сжатия = 50%. Минимальное количество символов в сообщении у турецкого языка. Минимальное количество символов в коде у ивритского и турецкого языков. Минимальное время выполнения кода у ивритского языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у ивритского языка.

Для 11 строки:

Среднее значение степени сжатия = 47%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у русского языка. Минимальное время выполнения кода у ивритского языка.  Минимальное количество символов, составляющих таблицу кодировки, у сербского, арабского, немецкого языков. Максимальная степень сжатия у немецкого языка.

Для 12 строки:

Среднее значение степени сжатия = 44%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у турецкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у итальянского языка.

АЛГОРИТМ ШЕННОНА-ФАНО

По аналогии с алгоритмом Хаффммана для алгоритма Шеннона – Фано были составлены таблицы для каждого из высказывания.

Для 1 строки:

Таблица 3.

Характеристики 1 строки на разных языках. Алгоритм Шеннона-Фано.

Среднее значение степени сжатия = 46%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у немецкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у арабского языка.

Для 5 строки:

Таблица 4.

Характеристики 5 строки на разных языках. Алгоритм Шеннона-Фано

Среднее значение степени сжатия = 43 %. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у белоруского языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у английского, французкого, итальянского языков.

Для 2 строки:

Среднее значение степени сжатия = 49%.Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у французкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у арабского языка.

Для 3 строки:

Среднее значение степени сжатия = 43%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у немецкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у арабского языка.

Для 4 строки:

Среднее значение степени сжатия = 43%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у немецкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у французкого и итольянского языков.

Для 6 строки:

Среднее значение степени сжатия = 46%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у греческого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у арабского и итальянского языков.

Для 7 строки:

Среднее значение степени сжатия = 51%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у французкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у итальянского языка.

Для 8 строки:

Среднее значение степени сжатия = 49%. Минимальное количество символов в сообщении у турецкого языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у немецкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у ивритского языка.

Для 9 строки:

Среднее значение степени сжатия = 64 %. Минимальное количество символов в сообщении у ивритского и арабского языков. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у французкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского и белорусского языков. Максимальная степень сжатия у арабского языка.

Для 10 строки:

Среднее значение степени сжатия = 49 %. Минимальное количество символов в сообщении у турецкого языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у французкого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у ивритского языка.

Для 11 строки:

Среднее значение степени сжатия = 46%. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у арабского языка. Минимальное время выполнения кода у сербского языка.  Минимальное количество символов, составляющих таблицу кодировки, у сербского, арабского, немецкого языков. Максимальная степень сжатия у немецкого языка.

Для 12 строки:

Среднее значение степени сжатия = 43 %. Минимальное количество символов в сообщении у ивритского языка. Минимальное количество символов в коде у ивритского языка. Минимальное время выполнения кода у греческого языка.  Минимальное количество символов, составляющих таблицу кодировки, у ивритского языка. Максимальная степень сжатия у итальянского языка.

СРАВНЕНИЕ АЛГОРИТМОВ

1. По итогам проведения анализа можно сделать вывод, что самым оптимальным по объему занимаемой памяти является ивритский язык. У него самое маленькое количество символов почти во всех характеристиках и в коде Хаффмана, и в коде Шеннона-Фано.
2. По времени ивритский язык не является самым эффективным, так как европейские языки обладают меньшим временем выполнения.
3. Также сравнивая время выполнения обработки сообщения на ивритском языке в двух алгоритмах, видно, что время выполнения в алгоритме Хаффмана меньше, чем в алгоритме Шеннона-Фано. Из чего можно сделать вывод, что алгоритм Хаффмана быстрее, чем алгоритм Шеннона-Фано.
4. Сравнивая количество символов в сообщении и в закодированной строке на ивритском языке, приходим к выводу, что в алгоритме Хаффмана требуется меньше памяти, чем в алгоритме Шеннона-Фано.
5. Для маленьких строк алгоритм Хаффмана быстрее для всех языков.
6. По итогам реализации кода, можно сказать, что кодирование по Хаффману отличается простотой кода программы: более легче и более нагляднее. 
7. По таблицам видно, что по степени сжатия алгоритм Хаффмана эффективнее.
8. Наибольшую степень сжатия дают итальянский и арабский языки.

ЗАКЛЮЧЕНИЕ

По итогам проделанной работы выявлено, что алгоритм Хаффмана более оптимальный по времени и по объему требуемой памяти, а также по степени сжатия данных. Причем на ивритском языке самое эффективное кодирование по требуемой памяти, а на арабском и итальянском языках наилучшая степень сжатия.