Нечеткая логика и ее преимущества при работе с базой данных

Аннотация. В последние годы все большее распространение получает нечеткая логика: ее применяют почти во всех областях науки и техники, например в системах искусственного интеллекта последнего поколения, а так же в экономике, медицинской диагностике. В статье приведены специальные термины и определения, рассмотрены примеры применения нечеткой логики в запросах к базам данных и описаны сильные и слабые стороны нечеткой и классической логик.

Ключевые слова: нечеткая логика; нечеткое множество; база данных; терм.

Введение

Раздел математики, получивший наименование нечеткой логики, представляет собой обобщенный вариант классической логики, а также теории множеств и основывается на понятии нечеткого множества. Познакомимся с данным вопросом поближе.

Своим появлением термин и понятие нечеткого множества обязаны американскому ученому Лотфи Заде, и в 1965 году были опубликованы в статье “fuzzy set”. Понятие нечеткого множества предполагает допущение, согласно которому функция принадлежности элемента множеству способна принимать как значения 0 или 1, так и все остальные значения множества [0,1].

Действительно, классическая логика, хорошо известная с очень древних времен, достаточно однообразна.  И если рассматривать ее в приближении, становится очевидным, что собой она представляет свод строгих правил, а также применение всего лишь двух значений – "истина" или "ложь". Данное положение обуславливает невозможность применения каких-либо других понятий в данном интервале, ровно так же, как двоичная логика использует только 0 и 1.

Не вызывает сомнения, что это обстоятельство – наличие только двух переменных - большое удобство для ЭВМ, но полная неприспособленность и недостаточность для характеристики ассоциативного человеческого мышления. Действительно, при условии, что все вопросы имеют только два ответа: “да” или “нет”, формулирование в двоичном мире собственных мыслей человека представляется невозможным.

Сегодня нечеткая логика получает все большее распространение, теперь ее можно встретить почти во всех областях науки и техники, в частности, в операциях по прочтении рукописного текста, системах искусственного интеллекта последнего поколения, автоматических системах управления новейшими автомобилями, экономике, медицинской диагностике.

Наиболее широкое использование нечетких запросов к базам данных получило в системах обработки информации последнего поколения. При этом, представляется целесообразным применять нечеткие запросы в базах данных, включающим в себя такие данные об объектах, к которым будут применены качественные критерии или нечетко сформулированные условия. Данный подход дает хорошую возможность для изложения запросов на естественном языке. Дело в том, что в текстовом запросе человека обычно наблюдается большое количество неточностей и неоднозначных формулировок. Прежде всего, это можно объяснить изобилием в языке множества слов с похожими значениями. Нечеткие запросы позволяют качественно исправить существующее положение дел.

Разберем пример применения нечеткой логики в запросах к базам данных, рассмотрим сильные и слабые стороны нечеткой и классической логик. Для объективного рассмотрения примем специальные термины и определения.

Основные термины и определения

Под понятием нечеткого множества будет скрываться математическое выражение нечеткой информации для выстраивания математических моделей. Суть понятия в том, что обладающие общим свойством элементы какого-либо множества, способны обладать общим свойством в разной степени, а значит, принадлежать данному множеству с разной степенью. Тогда формулировка вроде “элемент принадлежит данному множеству” становится бессмысленной, так как возникает потребность указать степень, с которой он удовлетворяет свойствам этого множества.

«Нечеткое подмножество Α некоторого универсального множества   характеризуется функцией принадлежности, которая ставит в соответствие каждому элементу число , принадлежащее интервалу , определяющее степень принадлежности элемента множеству Α» [1]. И чем больше степень принадлежности множеству Α, тем в большей степени элемент универсального множества будет соответствовать свойствам нечеткого множества .

Зададим нечеткое множество: :

«Нечеткая переменная будет характеризоваться набором , где  – является названием переменной,  – задает универсальное множество (область рассуждений),  – представляет нечеткое множество на »  [2].

«Лингвистической переменной является переменная, значениями которой могут быть слова или словосочетания как естественного, так и искусственного языка» [2].

«Терм–множеством является множество абсолютно всех возможных значений лингвистической переменной» [2].

«Термом является один из элементов терм–множества» [2]. Так, лингвистическая переменная "вес" способна принимать значения "тяжелый", "легкий", "средний".

Примеры

Рассмотрим пример на таком понятии как температура окружающей среды. Пусть имеется неточное определение "жаркая погода". Для кого-то температура воздуха 10°С будет считаться высокой, а кому-то  и в 20°С будет недостаточно тепло, но отметка на термометре в 35°С точно характеризует жаркую погоду. Конкретные границы определить практически невозможно, поэтому введем нечеткое множество для данного понятия:

Таблица 1.

Задание нечеткого множества “жаркая погода”

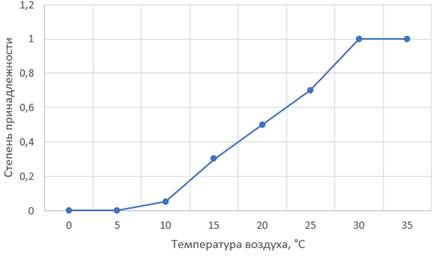
Рисунок 1. Графическое представление функции принадлежности множества "Жаркая погода"

В качестве еще одного примера можем рассмотреть расстояние от дома до университета. Для этого случая неточное определение будет звучать как "недалеко". Так, например, для некоторых студентов расстояние в два квартала кажется небольшим, однако все согласятся, что 200 метров от общежития до университета- наикратчайший маршрут. Так же, как и для первого случая точный порог определить практически невозможно поэтому нечеткое множество примет следующий вид:

Таблица 2.

Задание нечеткого множества “Недалеко”

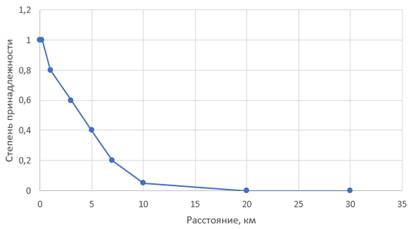
Рисунок 2.  Графическое представление функции принадлежности множества "Недалеко"

Из примеров видно, в чем проявляется суть нечеткого множества. Любой определенный случай можно перенести на конкретные числа в соответствующем масштабе.

Различие графических интерпретаций данных нечетких множеств не противоречит смысловой схожести примеров. Это доказывает, что вид функции принадлежности элемента множеству не играет ключевой роли, но для удобства вычислений принято использовать определенные аналитические функции, что является преимуществом при применении методов теории нечетких множеств. Наиболее широкое распространение получили трапецеидальная, треугольная и гауссовская функции принадлежности. В данной работе так же будут представлены z-подобные и s-подобные функции принадлежности.

Основное требование при построении функции принадлежности – как минимум одному лингвистическому терму должно соответствовать положительное значение функции.

Рассмотрим вышеупомянутые аналитические функции.

Трапецеидальная функция принадлежности.

Трапецеидальная аналитическая функция задается четырьмя параметрами . А её значение в определенной точке вычисляется по ниже приведенной формуле.

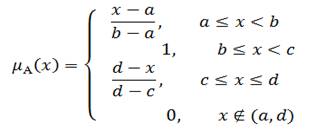
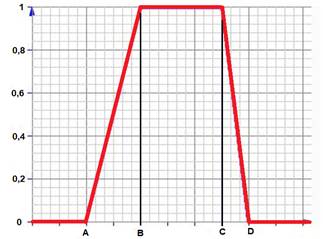
Рисунок 3. Трапецеидальная функция принадлежности

Важным свойством трапецеидальной функции является то, что она может принимать симметричный вид при условии .

Треугольная функция принадлежности.

Треугольная аналитическая функция задается тремя числами 

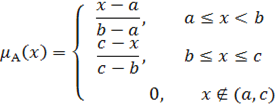
Рисунок 4. Треугольная функция принадлежности

Так же, как и трапецеидальная функция, треугольная аналитическая функция обладает свойством симметрии при 

Обе эти функции принадлежности обычно используются для описания неопределенностей типа "примерно равно", "находится в интервале".

Гауссовская функция принадлежности.

Гауссовская функция принадлежности задается двумя параметрами: с – определяет центр нечеткого множества, а σ – крутизну функции.

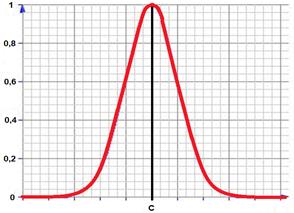
Рисунок 5. Гауссовская функция принадлежности

Рассмотрим также s-подобные и z-подобные функции принадлежности, используемые в данной работе.

S – подобная функция принадлежности.

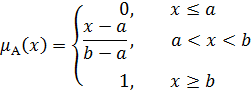
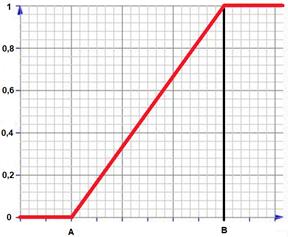
Рисунок 6. S-подобная функция принадлежности

Z -подобная функция принадлежности.

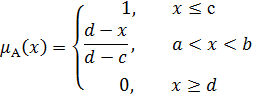
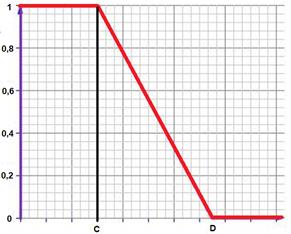
Рисунок 7. Z-подобная функция принадлежности

Операции над нечеткими множествами.

Над нечеткими множествами так же, как и над любыми другими можно совершать операции. Рассмотрим операции: дополнение, объединение, пересечение.

1. Дополнение.

Нечеткие множества А и В, заданные на универсальном множестве Х, дополняют друг друга, если при .

Рисунок 8. Дополнение нечеткого множества

2. Объединение.

Это наибольшее нечеткое множество, включающее в себя нечеткие множества A и B, заданные на универсальном множестве. 
.

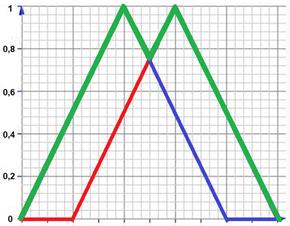
Рисунок 9. Объединение нечетких множеств

3. Пересечение.

Это наименьшее нечеткое множество, включающее в себя нечеткие множества A и B, заданные на универсальном множестве. 

.

Рисунок 10. Пересечение нечетких множеств

Применение нечеткой логики в запросах к базам данных.

В современном мире большое количество информации обрабатывается на вычислительных машинах. ЭВМ не могут анализировать эту информацию на языках, которые используются в обычной речи. Им нужна четко представленная числовая форма требуемой информации. В повседневной жизни, по причине неопределенности и неточности самой информации, человек, обращаясь к некоторой базе данных, не всегда способен сформулировать четкий, определенный запрос. Это и является главной проблемой, которая может быть решена применением нечеткой логики.

Допустим, требуется следующая информация, которую необходимо получить из базы данных: "Получить список мощных, но оптимальных по цене аудиосистем"

Таблица 3.

База данных аудиосистем

Любая аудиосистема имеет конкретное числовое значение в таких характеристиках, как выходная мощность RMS и цена, их можно конкретизировать с бесконечно большой точностью. Но приведенные высказывания «мощный» и «оптимальный» не имеют каких-то четких численных определений, поэтому вышеизложенное задание звучит довольно размыто и неточно.

Язык запросов SQL не предусматривает обработку данного запроса поэтому используем концепцию нечетких запросов.

Наглядно проиллюстрируем ограниченность четких запросов на примере. Допустим запрос пользователя выглядит следующим образом: «Купить аудиосистему не дороже 5000 рублей с выходной мощностью более 120 Вт».
В синтаксисе SQL это будет выглядеть так:

select Model from Audio_systems

where (Audio_systems.Price <= 5000 AND Audio_systems.Engine_Power > 120)
Из-за строгих ограничений четких запросов результатом поиска будет пустое множество, хотя аудиосистемы марок « Sony MHC-V21D » и « Hyunday H-MAC100» почти удовлетворяют условиям запроса. Нечеткие запросы расширяют границы поиска и, тем самым, решают проблему «исчезающей» информации. А значит пользователю будут предложены варианты, наиболее подходящие по заданным характеристикам.

Адаптируем четкий запрос к нечеткому: «Получить список аудиосистем со средней ценой и большой выходной мощностью RMS».

Введем лингвистические переменные «Цена» и «Выходная мощность».

Переменная «Цена» будет определена на интервале [500;∞] (допустим, что дешевле, чем за 500 руб. аудиосистему приобрести нельзя). Также объявим три лингвистических терма – «Низкая», «Средняя», «Высокая».  Построим функции принадлежности для каждого из них, используя функции трапецеидального и s-образного вида с параметрами:

«Низкая» = [500, 500, 2500, 3000], «Средняя» = [2500, 3500, 5000, 6000], «Высокая» = [5000, 6500].

Рисунок 11. Функция принадлежности для лингвистической переменной «цена»

Для наглядности вычислим степень принадлежности цены аудиосистемы в 5545 рублей к каждому из нечетких множеств:

Аналогично определим переменную «Выходная мощность». Её область определения: [0;200]. Лингвистические термы: «Ниже средней», «Средняя», «Выше средней», «Высокая». Зададим параметры функций принадлежности трапецеидального, s-образного и z-образного вида: «Ниже средней» = [50, 55], «Средняя» = [50, 55, 60, 70], «Выше средней» =[60, 70, 100, 120], «Высокая» = [110, 120].

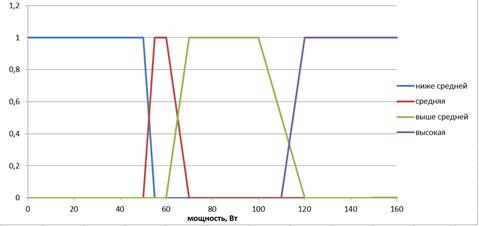
Рисунок 12. Функция принадлежности для лингвистической переменной «Выходная мощность»

На языке SQL наш запрос будет выглядеть так.

select Model from Audio_systems

where (Audio_systems.Price = “Средняя” AND Audio_systems.Engine_Power = “Большая”)

Результат запроса:

Таблица 4.

Результат запроса

Другие модели не попали в результат, поскольку для них значение функции принадлежности  Аудиосистема модели “Sony MHC-V21D” стоимостью 5125 Rub с выходной мощностью 125 Вт соответствует запросу с функцией принадлежности 0,92, что наиболее близко к с . На практике часто ограничиваются вводом порогового значения функции принадлежности. В результате, записи со значением функции ниже порогового не включаются в итоговой список.

Заключение

Использование нечеткой логики при формировании запросов к хранилищу данных позволяет расширить границы поиска и, тем самым, решить проблему «исчезающей» информации. Данный поход приведет к тому, что пользователю будут предложены варианты, наиболее подходящие условию запроса, потому что в нечеткой логике в отличие от четкой, границы поиска более размыты.  В статье были рассмотрены преимущества нечетких запросов, с помощью которых удалось увеличить взаимопонимание между человеком и машиной.