КАК ТЕОРИЯ КОЛМОГОРОВА АРНОЛЬДА МОЗЕРА И ХАОС ПРОЯВЛЯЮТ СЕБЯ В ЧЕЛОВЕЧЕСКОЙ ЖИЗНИ?

Аннотация. Определены понятия хаоса и порядка для использования в динамических системах. Даны определения динамических и гамильтоновых систем. Обнаружены основные различия между слабо диссипативной теорией КАМ и классической теорией. Рассмотрены примеры использования слабо диссипативной теории КАМ в практических целях. Показана зависимость системы от начальных условий.

Ключевые слова: Динамические системы, дифференциальные уравнения, численный расчет, хаос, порядок

Порядок и хаос:

Для начала давайте определим, что мы называем порядком и что такое хаос в этой статье.

Порядок — это предсказуемое поведение системы, которое может быть решено общим образом

Хаос – решается только численно, чувствительно к начальным условиям. [2]

Далее мы рассмотрим гамильтоновы системы, которые подчиняются следующей системе уравнений.

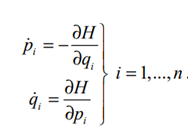
Где H - гамильтониан или интеграл энергии уровня. [1]

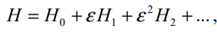
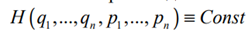
Теория Колмогорова-Арнольда-Мозера рассматривает объекты без потерь энергии. Примером такой системы является маятник без трения. Обратите внимание на фазовый портрет (рис. 1) – линии замкнуты; они показывают, что маятник возвращается в исходное положение. Две верхние кривые описывают более общий случай, когда маятник совершает полный оборот вокруг своей оси.

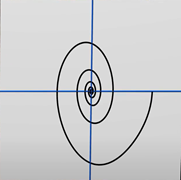
Рисунок 1. Фазовый портрет

Чтобы описать следующие примеры, нам нужна теорема Пуанкаре-Бендиксона: она гласит, что если мы рассматриваем не все векторное поле, а некоторую область и знаем, как оно ведет себя вокруг этой области, то траектории сходятся либо в устойчивое положение, либо в периодическую траекторию.

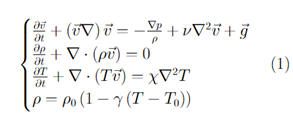
Система Лоренца. Лоренц упростил систему (1) и получил систему обыкновенных дифференциальных уравнений (2). Мы видим, как ведут себя решения упрощенной системы. Это хаотично, и видно, что есть три стабильных положения. Два цикла и одна точка 0,0,0.

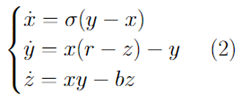
Рисунок 2. Графическое изображение

Такая система может описывать погодные условия. Н о поскольку это скоро войдет в цикл, необходимо постоянно менять начальные условия, иначе мы придем к циклу. Поэтому нет смысла прогнозировать погоду более чем на неделю вперед. Дальнейший прогноз более точен, если брать среднее арифметическое за последние годы. Следующий пример: задача о n телах является одним из наиболее важных примеров. Рассматривается наша Солнечная система. Вычислить движение Земли вокруг Солнца не проблема, если забыть о существовании других планет – в системе есть порядок. Но если мы добавим хотя бы Марс, то система вообще становится неразрешимой, и она переходит в царство хаоса. Теория Колмогорова-Арнольда-Мозера рассматривает не только движение объектов; ее основная идея заключается в рассмотрении траекторий. Улетит ли Юпитер к звезде Бетельгейзе? Поменяются ли Марс и Земля местами? Вот его основная суть. Но мы рассматривали системы без потерь энергии. И что произойдет, если мы добавим их слабые потери? Слабая диссипация в таких системах породила новую слабо диссипативную теорию Колмогорова-Арнольда-Мозера [2,3,4]. Вот основные отличия от классической теории КАМ:

1. СДТ КАМ применяется к системам, в которых есть слабая диссипация, тогда как классическая теория КАМ применяется к гамильтоновым системам без диссипации.

2. СДТ КАМ рассматривает не только регулярные орбиты, но также и стохастические орбиты, которые могут возникать в системах с диссипацией.

3. СДТ КАМ использует методы стохастической динамики, такие как усреднение Ландау-Лифшица, для изучения динамики систем с диссипацией.

Если перейти к формулам, то мы фактически "убьем" гамильтониан и напишем дифференциальное уравнение на H. [1]

В простейшем случае это выглядит примерно так (рис. 3). Обратите внимание на пример фазового портрета. Он уже становится все более непредсказуемым

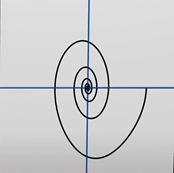
Рисунок 3. Фазовый портрет

Рассмотрим примеры: маятник с трением. Его фазовый портрет уменьшается по мере того, как сила трения уменьшает амплитуду и маятник приходит в устойчивое положение. Слабо диссипативная теория проявляется в намотанной трубке. Он обнаружил необычное явление: в центре струи газ, выходящий из циклона, имел более низкую температуру, чем исходная. WDT CAM позволяет рассчитать вихревой эффект в такой трубе. Не только в физике нашлось применение, но и в информатике. Система Бонхеффера-ван дер Поля, простейшая модель нейрона. Это также можно исследовать с помощью WDT CAM. Экономика, биология, информатика, физика... теория Колмогорова-Арнольда-Мозера и ее слабо диссипативная версия очень распространены.

В докладе рассматриваются динамические системы и их важность. Казалось бы, за таким странным названием скрывается связь с нашим миром и вполне привычными вещами.