Исследование методом операционного исчисления влияния вращения Земли на свободное падение тел
Секция: Физико-математические науки

XLI Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
Исследование методом операционного исчисления влияния вращения Земли на свободное падение тел
Исследуем свободное падение материальной точки вблизи земной поверхности. Свяжем систему координат с положением тела, где ось z направлена по вертикали вверх, ось x – по касательной к окружности радиуса h (перпендикулярно к плоскости рисунка на нас), а ось y – в плоскости меридиана (в плоскости рисунка). Направление линии действия силы тяжести Р называется вертикальным направлением в данной точке земной поверхности. Угол ![]() , образуемый вертикальным направлением с экваториальной плоскостью, называется географической широтой в данной точке земной поверхности.
, образуемый вертикальным направлением с экваториальной плоскостью, называется географической широтой в данной точке земной поверхности.

Будем рассматривать свободное падение тела вблизи поверхности Земли, поэтому считаем, что сила тяжести ![]() и широта
и широта ![]() постоянны.
постоянны.
Система уравнений, спроецированных на оси координат, при начальных условиях 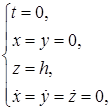 имеет вид [3]:
имеет вид [3]:
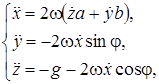
где ![]()
![]()
В [1] рассматривается решение данной системы с помощью степенных рядов.
В данной работе делается попытка решения этой задачи методом операционного исчисления [4; 5; 2].
Перейдем к изображениям:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Применим преобразование Лапласа к каждому из уравнений системы:
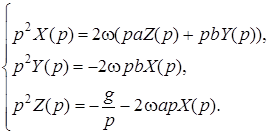
Для нахождения изображений неизвестных функций ![]() , Y(р) и Z(p) решим систему следующих операторных уравнений:
, Y(р) и Z(p) решим систему следующих операторных уравнений:
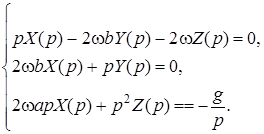
По правилу Крамера имеем:
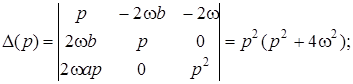
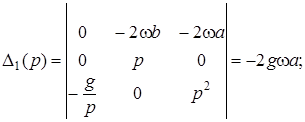

![]()
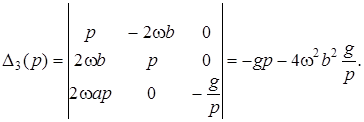
Следовательно, изображения имеют вид:

Таким образом, получены следующие уравнения движения:

Разложив полученные уравнения в ряд по ![]() имеем:
имеем:

При ![]() система примет вид:
система примет вид:

что согласуется с решением, полученным в [1].
Таким образом, траектория свободно падающего тела лежит в плоскости, перпендикулярной меридиану. Первое уравнение полученной системы указывает на отклонение тела от вертикали в сторону отрицательного отчета координаты х, т.е. с запада на восток.
Оценим отклонение материальной точки от осей координат на широте Нижнего Тагила, т.е. при ![]() g=9,81 м /сек2, при падении с высоты 12000 метров.
g=9,81 м /сек2, при падении с высоты 12000 метров.
Имеем:

Таким образом, при свободном падении с высоты h=12000 м на широте Нижнего Тагила материальная точка отклонится в восточном направлении на 15,09 м.





