Исследование колебаний струн музыкальных инструментов

Аннотация. Данная статья посвящена исследованию колебаний струн музыкальных инструментов. Проанализированы уравнения поперечно-продольных колебаний гибкой натянутой струны. Получены осциллограммы частот колебаний струн. Проведен сравнительный анализ частот и периодов колебаний по графикам их зависимостей с помощью преобразования Фурье. Обнаружены характерные особенности взаимосвязи частот колебаний двух музыкальных инструментов.

Ключевые слова: колебания, волны, частота, период, осциллограмма, музыкальный инструмент, гитара, струна, график.

Колебания – это изменения состояния физического тела, обладающие определённой степенью повторяемости во времени. Звуковые колебания возникают при изменении плотности воздуха, т.е. в результате разрежений или сгущений в воздушной среде. Для возникновения любых колебаний необходим источник или сила, которая их создаёт.

К струнным музыкальным инструментам относятся скрипка, виолончель, альт, контрабас, арфа, гитара, гусли, балалайка, домра. Все струнные инструменты передают колебания от одной или нескольких струн воздуху через свой корпус или через звукосниматель в случае с электронными инструментами. Струнные музыкальные инструменты разделяются по технике воздействия на струну, распространённые техники – это щипок, действие смычка и удар.

В данной статье исследуются колебания струн двух музыкальных инструментов - гитары и балалайки. Цель работы: определение собственных частот колебаний струн гитары и балалайки, получение графиков зависимостей частот и периодов колебаний струн с помощью электронного осциллографа для их последующего сравнения и анализа. При решении задач исследования были изучены работы [1-7].

Для изучения колебаний струн музыкальных инструментов в работе использовали классическую шестиструнную гитару и балалайку-прима. Гитара – струнный щипковый музыкальный инструмент с натянутыми струнами, с помощью которого получают звуки разной частоты (рис. 1).

Рисунок 1. Классическая испанская гитара (строй гитары e, h, g, d, a, e) и расположение нот по ладам балалайки (строй e, h, g)

Балалайка в свою очередь представляет собой щипковый струнный музыкальный инструмент с треугольной декой. Для гитары и балалайки существует несколько видов настройки струн (рис. 1).

Под струной в акустике понимают однородную тонкую гибкую упругую нить, представляющая собой колебательную систему с распределенными параметрами. В результате изменения вертикальной составляющей произвольного элемента струны, проявляются силы, воздействующие на соседние участки и струна начинает движение в вертикальной плоскости; и возникшее колебание бежит по струне - поперечные бегущие волны (рис.2), распространяются в обе стороны от точки воздействия на струну.

Рисунок 2. Поперечные волны на струне

Уравнение распространения поперечных волн в струне определяется следующим выражением:

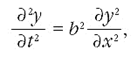                                                                                                               (1)

где x, y – координата продольной и поперечной колеблющейся точки на струне, t – время колебания струны, b – скорость распространения колебаний.

Решение уравнения двух бегущих волн:

                                                                                                      (2)

Поперечные свободные колебания струны могут быть представлены в виде:

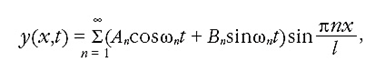                                                                                      (3)

где l – длина струны, ω_n = π·n·b/l – частота колебаний, А_п, В_п – амплитуда колебаний струны, n – число колебаний [1-2].

Струна инструмента, в процессе своего движения, смещается поперек первоначального положения и испытывает дополнительные деформации – растяжение и сжатие. «Возникающие силы Т в струне определяются отношением: 

Т = F / 2·sinα,                                                                                                                 (4)

где F – действующая сила на струну, α – угол отклонения струны от первоначального положения».

«Поперечные возникающие силы оказываются источником продольных движений корпуса и струн. Они будут раскачивать деку музыкального инструмента и станут основным источником звука.

Согласно формулам (1-4) получим уравнения поперечно-продольных колебаний гибкой предварительно натянутой струны:

                                                                              (5)

где b, а – скорости поперечных и продольных волн, е₀ – первоначальная деформация струны. Уравнения (5) позволяют теоретически описать колебания струн в продольном и поперечном направлении» [2].   

Для проведения практических измерений параметров колеблющихся струн применялось следующее оборудование: персональный компьютер, шестиструнная классическая гитара, гитарный тюнер Korg, балалайка-прима, микрофоны, микшерный пульт, предусилитель, пьезодатчик, система соединительных проводов, студийные наушники, компьютерная программа - электронный осциллограф Frequency Analyzer (рис. 3).

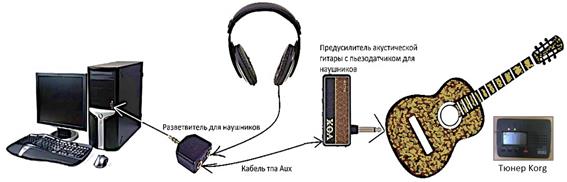
Рисунок 3. Схема подключения звукозаписывающей аппаратуры

Запись акустической гитары начинали с настройки инструмента, строй гитары классический – (e, h, g, d, a, e) и строй балалайки-прима – (e, e, a). Проверка настройки музыкальных инструментов производилась с помощью гитарного тюнера Korg [3, 4].

Для записи акустической гитары использовали конденсаторный микрофон, который располагали на расстоянии 30-40 см рядом с отверстием резонатора инструмента, также применяли пьезодатчики (рис.4).

Рисунок 4. Подключение гитары к компьютеру с помощью пьезодатчика и запись колебания струн с помощью компьютерной программы

Измерив частоту колебания струн для каждого инструмента получили значения частот в соответствии с присвоенными нотами (рис. 5).

Рисунок 5. Строй гитары и балалайки, полученный в экспериментах

Было установлено, что строй гитары и балалайки (рис. 5), полученный в экспериментах практически совпадает с табличным значением строя (рис. 6) исследуемых музыкальных инструментов [5-6].

Рисунок 6. Стандартный строй гитары по классической испанской настройке (в кварту и увеличенную квинту)

Построенные диаграммы, на основе значений частот колебания струн с помощью программы Frequency Analyzer осциллограммы для каждой струны, позволили провести анализ тонов музыкальных инструментов (рис.7).

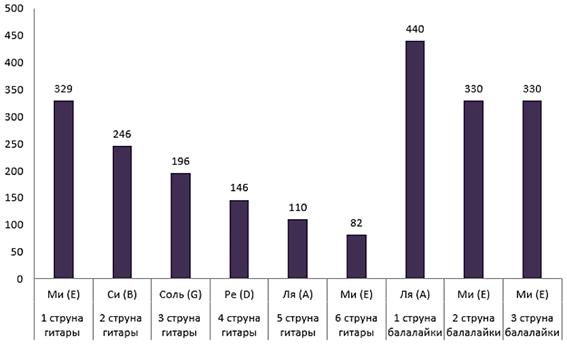
Рисунок 7. Диаграмма частот колебаний струн гитары и балалайки

Программа Frequency Analyzer представляет собой Open Source амплитудно-частотный звуковой анализатор, действующий в режиме реального времени. Эта программа позволяет работать с любыми звуковыми колебаниями, включая человеческий голос, выполняя над ними быстрое преобразование Фурье и разбивая их на частотные составляющие.

Когда микрофон преобразует звуковые колебания в электрическое напряжение, звуковая карта работает как цифровой вольтметр, измеряющий напряжение от 11030 до 44000 раз в секунду. Каждая измеряемая величина преобразуется в восьми- или шестнадцатиразрядное число. В результате выборки удаётся получить ряд чисел; и звук может быть показан в виде комбинации синусоидальных волн различных частот, математически это разделение на составляющие частоты называется преобразованием Фурье [7].    Программа «Frequency Spectrum» позволяет получить графическое представление спектрального состава звука (рис. 8).

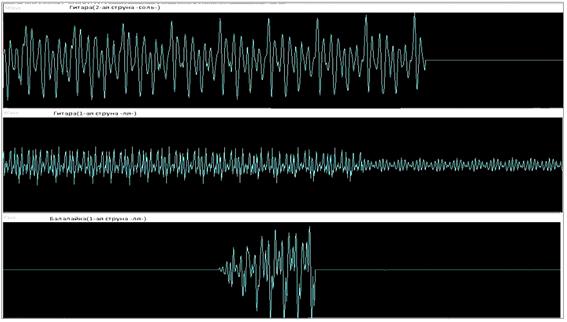
Рисунок 8. Осциллограммы колебаний 1 и 2 струн гитары и балалайки

Получив осциллограммы для 1 струны балалайки было выявлено то, что частоты соответствуют гармоникам 1-ой струны гитары. В экспериментах использовали балалайку - прима, у которой вторая и третья струна - это нота “Ми”; эта нота по частоте совпадает с 1 струной гитары ноты “Ми”, как и видно из общей диаграммы (рис.8, 9). Из графиков зависимостей видно, что первая струна “Ля” имеет большую частоту и амплитуду колебаний, но при этом наименьший период колебаний (рис. 9, 10).

Рисунок 9. Осциллограммы колебаний 3-6 струн гитары зафиксированные электронным осциллографом Frequency Analyzer

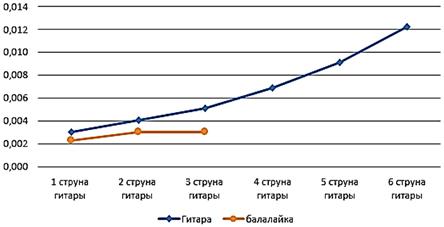
Рисунок 10. Период колебаний струн гитары и балалайки

В результате экспериментов была подтверждена зависимость амплитуды звуковых колебаний от частоты, были исследованы резонансные явления, связанные с совпадением частот обертонов колебаний в поперечном направлении с частотами вынужденных продольных колебаний струн.

При создании музыкальных инструментов изучаются колебания струн, движения пластин и мембран инструментов, что позволяет изучать и практически применять обнаруженные акустические эффекты, вызванные взаимным влиянием различных типов колебаний и волн. Результаты исследований в данной работе могут быть использованы для конструирования новых электронных музыкальных инструментов.