Использование методов математической статистики для научных и практических целей

Практически ежедневно мы используем в своём лексиконе такие слова как «случайность», «вероятностно это произойдет», «вполне возможно». И зачастую редко задумываемся о математической подоплёке произносимого. И только начав обучение в Курской государственной сельскохозяйственной академии по специальности Экономика и бухгалтерский учет, мы в процессе изучения теории вероятности и математической статистики увидели на практических примерах, что это важнейшая наука, направленная на изучение случайных, не подлежащих строгому математическому описанию, событий и явлений, их свойств, закономерностей и взаимосвязей. Другими словами, практически любые выводы, сделанные статистикой, рассматриваются как вероятностные [1]. Особенно наглядно вероятностный характер статистических исследований проявляется в выборочном методе, поскольку любой вывод сделанный по результатам выборки оценивается с заданной вероятностью.

Проведя анализ литературы заданной тематики, мы может отметить широкий спектр использования методов теории вероятностей в экономике, теории информации, в теории принятия решений, в физике, астрономии и других дисциплинах. Мы согласны с высказыванием Микрюковой Е.Ю. о том, что в работе специалиста любого профиля неоспорима актуальность использования методов математической статистики, «благодаря которым появляется возможность проанализировать объемный массив информации, учесть различное количество факторов, а также получить содержательный вывод по обработанному материалу» [2, с.208]. Но особенно нас заинтересовала тематика использования теории вероятности с точки зрения методов сбора, анализа и обработки результатов статистических данных наблюдений для научных и практических целей. Другими словами, изучение совокупности однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Следовательно, для более детального изучения данного вопроса, основная наша задача заключается в исследовании всей совокупности по выборочным данным в зависимости от поставленной цели, т.е.: закона распределения, числовых характеристик и т.д. для принятия управленческих решений в условиях неопределенности.

В России 2020 год был объявлен годом здоровья. Двигательная активность является неотъемлемой частью сохранения здоровья человека. По данным Росстата избыточный вес наблюдается у 15% подростков и более чем у 30% детей до 13 лет; среди взрослых ожирением страдает каждый пятый. Молодые люди в возрасте 15-18 лет все меньше занимаются спортом и физическими упражнениями и все больше времени уделяют компьютерным играм, чатам в Интернете. Неутешительный факт - ожирение является болезнью 21 века, с которой нужно бороться, как можно быстрее.

Мы решили исследовать масштабы данной проблемы ограничившись образовательным пространством нашей академии, а именно проведя исследование среди первокурсников факультета СПО. В анкетировании приняли участие 50 человек в возрасте 15-16 лет.  

Итак, опираясь на выборочную совокупность, введем обозначения: Хi –вес опрашиваемых, ni - количество студентов. В результате нами были получены следующие данные:

Согласно поставленной задачи, нам необходимо найти: а) среднее X, среднее квадратическое отклонение S и коэффициент V; б) построить гистограмму и полигон частот.

Для решения поставленной задачи перейдем к простому вариационному ряду, выбирая в качестве значений середины интервалов. Получим:

Найдем необходимые числовые характеристики. Выборочная средняя:

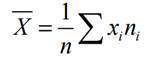
Х=*(45*12+55*15+65*9+75*7+85*4+95*3)=62

Выборочная дисперсия

S²=*((45-62)²*12+(55-62)²*15+(65-62)²*9+(75-62)²*7+(85-62)²*4+(95-62)²*3)=*(289*12+49*15+9*9+169*7+529*4+1089*3)=217

Выборочное среднеквадратичное отклонение:

S14,73

Какую часть среднеквадратическое отклонения составляет от среднего арифметического в процентах показывает коэффициент вариации, который рассчитывается следующим образом:

V

Все вышеуказанные расчёты представим в табличной форме:

По данным расчётов построим гистограмму и полигон частот

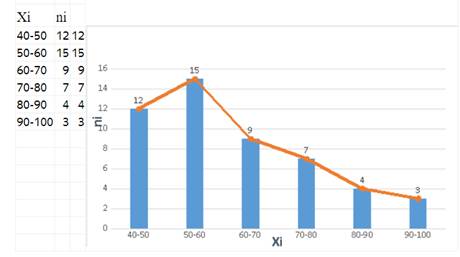
Рисунок. Гистограмма

Как показывают математические расчеты, ситуация на нашем факультете, в рамках обозначенной ранее проблемы, не критична. На основе полученных данных были проведены тематические беседы рекомендательного характера.

С другой стороны, всестороннее изучение теории вероятности и математической статистики с точки зрения обучения будущих экономистов направлено на, как верно подмечено Пожидаевой Е.Ю., «достижение должного уровня образованности, представляющей собой своеобразный синтез компетентностей, формируемой с учетом освоения элементарной и функциональной математической и информационной грамотности» [3, с.265]. На конкретном примере мы продемонстрировали, что изучение случайных процессов по результатам наблюдений целесообразнее проводить при помощи математической статистики, дающей возможность построения научно-обоснованных выводов и рекомендаций.