Интерпретация семейства золотых констант последовательностей a(n)=ka(n–1)-(n–2) в виде матриц новемологической таблицы
Секция: Физико-математические науки

I Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Интерпретация семейства золотых констант последовательностей a(n)=ka(n–1)-(n–2) в виде матриц новемологической таблицы
В век информационных технологий требуется запоминать огромное количество информации, которые требуют нового подхода запоминания. Одним из рациональных методов запоминания это применение новемологической таблицы в виде девятеричных группировок данных. Этими данными могут быть формулы, ключевые слова, термины, константы и т. д. Интегративная способность матриц новемологической таблицы предусматривает трансформацию равновесной со всех сторон базовой матрицы (магического квадрата) на одноуровневую сферическую поверхность вращения девяти частиц по форме двукратно-лепестковой восьмерки. По данной модели устроена фундаментальная динамика частиц ядра атома и заложена в основу работы квантового компьютера.
Базовая матрица новемологической таблицы на плоскости имеет вид:
|
4 |
9 |
2 |
|
3 |
5 |
7 |
|
8 |
1 |
6 |
Сумма элементов по строкам, столбцам и диагоналям составляет число 15. Данная матрица составлена по принципу вращения движения элементов без «столкновений» на перекрестках. Если спроецировать данную матрицу в трехмерное пространство, то получится куб, в котором нижние элементы составят элементы первого уровня, элементы второй строки составят элементы второго уровня, и верхние элементы составят элементы третьего.
Запись натуральных чисел до 81 в виде новемологической таблицы, состоящая из девяти базовых матриц имеет вид (табл.2):
Таблица 2.
Новемологическая таблица из девяти базовых матриц

Найдем коэффициент изменения уровней к1= 369:126=2,928571 как отношение суммы строк первого уровня к сумме строк второго уровня, к2 = 612:369=1,65853 как отношение суммы строк второго уровня к сумме строк третьего уровня. Найдем коэффициент изменения к3= 69 : 42 = 1,6428 как отношение суммы строк третьей базовой матрицы первого уровня к сумме строк второй базовой матрицы первого уровня.
Для констант целочисленных последовательностей, члены которых заданы рекуррентными соотношениями a(n)=±ka(n–1)–(n–2), возможен вариант квадратных уравнений, которые имеют вид X2–kX+1=0, приводит к соотношению: X+1/X=k. Отсюда следует: 1/X = k – X. Число k является ближайшим к константе последовательности целым числом. Как видим, константы последовательностей обладают таким же свойством, что и золотая пропорция в четной степени – обратные значения констант в точности равны числу, дополняющему их до ближайшего целого числа. Например, последовательность, имеющяя рекуррентную формулу a(n)=10a(n–1)–a(n–2) при a(0)=2 и при a(1)=10 порождает последовательность вида: K(n) = 2, 10, 98, 970… В энциклопедии Нейла Слоэна она зарегистрирована под номером A087799 [1,2,3]. Золотые константы и их обратные значения для последовательностей, члены которых заданы рекуррентными соотношениями a(n)=ka(n–1) – (n–2), приведены в табл.3[1,2,3]. Найдены золотые константы х30 по х81 как корни уравнения х2-kх+1=0, при к= 30, 31,32…. 79, 80, 81 с помощью Excel. Таблицу золотых констант последовательностей вида a(n)=ka(n–1)-(n–2) перепишем по принципу новемологического распределения по 9-ти секторам, а именно по принципу «снизу-вверх», «слева-направо» (табл.3):
Таблица 3.
Новемологическая таблица золотых констант

Запишем данную таблицу по принципу новемологического распределения по 9-ти секторам и уровням (табл.4):
Таблица 4.
Новемологическая таблица золотых констант по 9 секторам и уровням
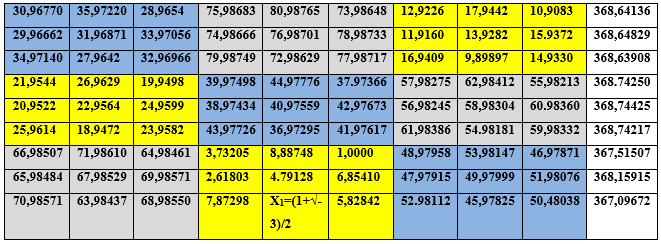
Заметим, что:
Сумма строки первого уровня матриц составляет в среднем  сумма строки второго уровня матриц составляет в среднем
сумма строки второго уровня матриц составляет в среднем  третьего уровня
третьего уровня 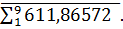 Найдем коэффициент изменения к1=
Найдем коэффициент изменения к1=  :
:  =2,928571 как отношение суммы строк первого уровня к сумме строк второго уровня, к2 =
=2,928571 как отношение суммы строк первого уровня к сумме строк второго уровня, к2 = 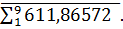 :
:  =1,65994 как отношение суммы строк второго уровня к сумме строк третьего уровня. Следует иметь в виду интересное совпадение коэффициентов изменения новемологической таблицы натуральных чисел, состоящая из девяти базовых матриц изменения к1= 369:126=2,928571, к2 = 612:369=1,65853 (табл.2). Найдем коэффициент изменения к3= 68,8668 : 41, 7736 = 1,6485 как отношение суммы строк третьей базовой матрицы первого уровня к сумме строк второй базовой матрицы первого уровня. Заметим, что такой же коэффициент к3= 1,6485 получен в отношениях соответствующих матриц новемологической таблицы натуральных чисел. Данные коэффициенты выполняются во всех остальных базовых матрицах.
=1,65994 как отношение суммы строк второго уровня к сумме строк третьего уровня. Следует иметь в виду интересное совпадение коэффициентов изменения новемологической таблицы натуральных чисел, состоящая из девяти базовых матриц изменения к1= 369:126=2,928571, к2 = 612:369=1,65853 (табл.2). Найдем коэффициент изменения к3= 68,8668 : 41, 7736 = 1,6485 как отношение суммы строк третьей базовой матрицы первого уровня к сумме строк второй базовой матрицы первого уровня. Заметим, что такой же коэффициент к3= 1,6485 получен в отношениях соответствующих матриц новемологической таблицы натуральных чисел. Данные коэффициенты выполняются во всех остальных базовых матрицах.
При записи таблицы золотых констант по принципу новемологического распределения по 9-ти секторам и уровням (табл.4) сумма строк составляет одинаковую сумму, в среднем  что показывает выполнение всех условий новемологического распределения. Данные коэффициенты выполняются во всех остальных базовых матрицах, что показывают выполнение условий новемологического распределения. Интерпретация числовых инвариантов последовательностей a(n)=ka(n–1)-(n–2) в виде матриц новемологической таблицы сохраняет все свойства новемологической записи.
что показывает выполнение всех условий новемологического распределения. Данные коэффициенты выполняются во всех остальных базовых матрицах, что показывают выполнение условий новемологического распределения. Интерпретация числовых инвариантов последовательностей a(n)=ka(n–1)-(n–2) в виде матриц новемологической таблицы сохраняет все свойства новемологической записи.





