Решение задачи о максимальном потоке в информационных сетях
Конференция: XLV Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Физико-математические науки

XLV Студенческая международная научно-практическая конференция «Молодежный научный форум»
Решение задачи о максимальном потоке в информационных сетях
Введение
В последние десятилетия сетевые технологии обретают все большую актуальность, и уже сейчас возможность решать различные задачи, возникающие в информационных сетях, является одной из самых важных задач компьютерных и кибернетических наук.
Информационная сеть – коммуникационная сеть, в которой информация выступает в качестве продукта создания, переработки, хранения и использования. С помощью теории графов такую сеть можно описать как ориентированный граф G = (V, E), в котором каждая дуга (i, j) ∈ E имеет пропускную способность cij ≥ 0 и поток fij. Потоком из s в t в сети G называется функция f: E → ℝ, удовлетворяющая условиям:
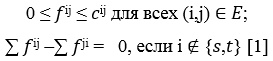
Целью данной работы стала программная реализация алгоритма проталкивания предпотока для решения задачи и сравнение его с алгоритмом Форда-Фалкерсона
Постановка задачи
Пусть у нас имеется сеть из вычислителей. Нам необходимо узнать, какую максимальную нагрузку в этой сети мы можем подать для решения задачи, поступающей на вход.
V – множество вычислителей, E – множество каналов, которые связывают вычислители.
1. Сеть состоит из n вычислителей
2. qi ∈ R+ - уровень загрузки i-го узла, i∈V
3. Связи между узлами имеют ограниченные пропускные способности. Будем считать, что эти связи задаются cij ∈ R, cij≥0 отлично от нуля только в том случае, если связь существует и обозначает в этом случае пропускную способность связи от агента i агенту j, (i,j) ∈E
4. uij количество передаваемой нагрузки по каналу (i →j), (i,j) ∈E
5. s – вход, t – выход сети
При этом должны выполняться условия:
1. 0≤uij≤cij
2. ∑uij - ∑uji = 0
Для решения этой задачи используем алгоритм проталкивания предпотока.
Для решения этой задачи используем алгоритм проталкивания предпотока.
Сначала введем несколько определений
Предпотоком будем называть функцию f:V×V→R, удовлетворяющую следующим свойствам:
1. fij=−fji (антисимметричность)
2. fij⩽cij (ограничение пропускной способностью)
3. ∀j∈V∖{s,t} ∑v∈Vfji⩾0 (ослабленное условие сохранения потока)
В условиях нашей задачи uij = fij. Т.е. найдя максимальный поток, мы найдем максимальную нагрузку.
Вершина j∈V∖{s,t} будет называться переполненной, если qj>0.
Функция h:V→Z+ называется высотой вершины, если она удовлетворяет условиям:
1. h(s)= n+2
2. h(t)=0
3. ∀(i,j)∈E, h(i)⩽h(j)+1
Операция проталкивания осуществляется только в двух случае, удовлетворяющим условиям
1. qi>0
2. h(i)= h(j)+1
3. i ≠ s и i ≠ t
Операция проталкивания может выполняться, как i→j, так и j→i. Главным условием является (i,j) ∈ E, либо (j,i)∈E
Алгоритм:
1 Пускаем максимальную нагрузку uij со входа s по всем возможным каналам. Т.е. предпоток fsj= csj, для всех (s,j) ∈E, а qj = ∑v∈Vfji
2. Просматриваем все вершины и производим операцию проталкивания
3. Если нет возможности провести операцию проталкивания, то выполняем операцию поднятия вершины h(i) = h(i)+1
4. Повторяем пункты 2 и 3 до тех пора, пока операция проталкивания или операция поднятия вершины станут невозможны для всех вершин.
Пример
Пусть дана сеть такого вида. На графе изображены значения cij.
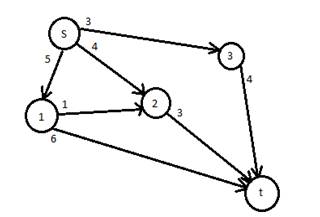
Рисунок 1. Сеть
Шаг 1.
Уровни загрузки вершин q1=5, q2=4, q3=3
Количество передаваемой нагрузки us1 = 5 us2=4 us3=3
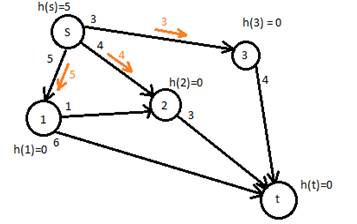
Рисунок 2. шаг 1
Шаг 2.
Т.к. нет возможности провести операцию проталкивания, то мы производим операцию поднятия, про производим операцию поднятия вершины
Уровни загрузки вершин q1=5, q2=4, q3=3
Количество передаваемой нагрузки us1 = 5, us2=4, us3=3
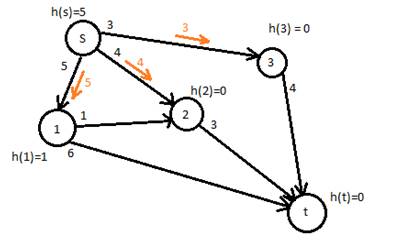
Рисунок 3.шаг 2
Шаг 3.
Производим операцию проталкивания
Уровни загрузки вершин q1=0, q2=4, q3=3
Количество передаваемой нагрузки us1 = 5, us2=4, us3=3, u1t =5
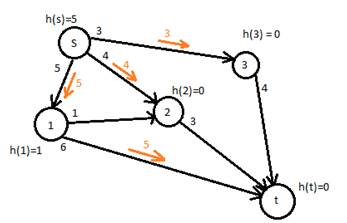
Рисунок 4. шаг 3
Так проделываем, пока операция проталкивания или поднятие вершины станет невозможной.
Конечный результат будет выглядеть следующим образом
Уровни загрузки вершин q1=0, q2=0, q3=0

Рисунок 5. конечный результат
Реализация алгоритма и сравнение его с алгоритмом Форда-Фалкерсона
Главным недостатком алгоритма Форда-Фалкерсона является то, что он может не работать при нецелочисленных значениях пропускных способностей. Более того может зацикливаться.[1] Этот недостаток у метода проталкивания предпотока отсутствует. Далее приведено сравнение времени работы этих двух алгоритмов (см. таблица 1).
Для проверки алгоритма Форда-Фалкерсона была использована программа, взятая с GitHub.[2]
Таблица 1
Сравнение времени работы двух алгоритмов
|
Количество вершин |
Время работы, сек |
|
|
Алгоритм проталкивания предпотока |
Алгоритм Форда-Фалкерсона |
|
|
10 |
0.0001 |
0.001 |
|
15 |
0.0004 |
0.003 |
|
20 |
0.0007 |
0.005 |
|
25 |
0.001 |
0.010 |
|
30 |
0.007 |
0.013 |
|
35 |
0.009 |
0.014 |
|
40 |
0.009 |
0.016 |
|
43 |
0.010 |
0.019 |
|
45 |
0.014 |
0.020 |
|
50 |
0.021 |
0.070 |
|
55 |
0.089 |
0.098 |
|
60 |
0.115 |
0.207 |
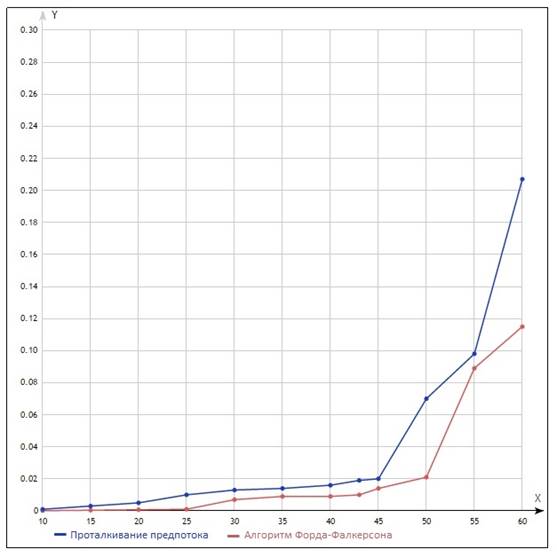
Рисунок 6. Сравнение двух алгоритмов
Выводы: Нами был реализован алгоритм проталкивания предпотока на языке С++. Этот алгоритм работает лучше для нашей задачи, чем алгоритм Форда-Фалкерсона. Учитывая, что алгоритм Форда-Фалкерсона может не работать на нецелочисленных значениях, оптимальнее всего использовать алгоритм проталкивания предпотока.
Листинг программы
const int N = 2000;
int e[N], c[N][N], h[N], n, s, t;
void polozgit(int f, int s) {
int q = min(e[f], c[f][s]);
e[f] -= q; e[s] += q;
c[f][s] -= q; c[s][f] += q;
}
void podnuat(int f){
int min = 3 * n + 1;
for (int i = 0; i < n; i++)
if (c[f][i] && (h[i] < min))
min = h[i];
h[f] = min + 1;
}
void discharge(int f){
int s = 0;
while (e[f] > 0){
if (c[f][s] && h[f] == h[s] + 1){
polozgit(f, s);
s = 0;
continue; }
s++;
if (s == n){
podnuat(f);
s = 0; }
}
}
void chitat(){
cin >> n >> s >> t;
srand(time(0));
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++){
if (i == j)
continue;
cin >> c[i][j]; }
}
void vbiv(){
chitat();
for (int i = 0; i < n; i++) {
if (i == s)
continue;
e[i] = c[s][i]; c[i][s] += c[s][i]; }
h[s] = n;
}
int main(int argc, char *argv[]){
list<int> l;
list<int>::iterator tec;
int star;
vbiv();
for (int i = 0; i < n; i++)
if (i != s && i != t)
l.push_front(i);
tec = l.begin();
time = clock();
while (tec != l.end()) {
star = h[*tec];
discharge(*tec);
if (h[*tec] != star)
l.push_front(*tec); l.erase(tec); tec = l.begin();
tec++; }
cout << "\nMax weight = " << e[t] << "\n";
return 0;
}





