Модель динамики численности популяции Мальтуса

Одним из глобальных вопросов современности требующих пристального внимания и принятия конкретных решений является опасность перенаселения нашей планеты людьми. Мировые ученые экономисты еще в VXIII веке затронули и подняли эту тему для обсуждения, обсуждая концепцию «мальтузианской ловушки», ее реальность и возможные последствия [3].

Математические модели, которые описывают процессы рождаемости и вымирания населения, называются демографическими моделями.

Они предназначены для описания преимущественно математическими методами населения и изменений в нем, процессов воспроизводства в целом или в отдельных его направлениях [1].

Понятие «моделирование» стало широко распространяться и применяться в демографии с 40-х гг. ХХ века. Модели в большинстве не охватывают всех процессов и учитывают лишь важнейшие характеристики явления. Так, модели воспроизводства населения рассматривают дифференциацию населения по полу и возрасту и т.п. В основе модели лежит формализация объекта моделирования, который описывается набором количественных и качественных характеристик.

В далеком 1798 году английский священник, ученый в области экономики и демографии Томас Роберт Мальтус (1766-1834 гᴦ.) выдвинул прославившую его теорию и создал работу под названием «Опыт о законе народонаселения в связи с будущим совершенствованием общества». Его труд вызвал горячие споры и большой интерес общественности.

Основная идея мальтузианской теории заключается в том, что народонаселение Земли слишком быстро увеличивается по отношению к производству необходимого количества пропитания. Неконтролируемый рост совокупности людей приведет к истощению плодородных почв и опасному перенаселению планеты. Его гипотеза указывала на геометрическую прогрессию роста неконтролируемой популяции в сравнении  с арифметической прогрессией роста источников существования.

По теории А. Смита рост численности населения считался явлением положительным, т. к. это и увеличение количества производителей, а значит и всеобщее обогащение.

Однако Мальтус озвучил, что люди еще и потребители, а значит увеличение спроса дополнительная экономическая проблема. Ученый предлагал снижать уровень рождаемости среди бедняков отменой материальной помощи и повышением уровня образования [3].

Беспечное отношение к вопросу рождения детей среди бедных слоев беспокоило как самого ученого, так и его сторонников. Они считали, что лишь люди, имеющие высокий достаток и статус в обществе, могут позволить себе большое потомство, однако, все совсем наоборот, чем выше уровень благополучия, тем ниже рождаемость.

Несмотря на то, что экономическая теория рассматривает народонаселение в качестве главного источника трудовых ресурсов и субъектом потребления, Т. Мальтус настаивал на жестком регулировании роста рождаемости, иначе считал он, абсолютное перенаселение будет неизбежным. В таких естественных факторах уменьшения плотности населения как война, болезни и эпидемии, голод, природные стихии он видел благостное спасение.

Меры борьбы, с ростом населения предложенные Мальтусом заключались в снижение рождаемости, особо это касалось низших слоев, так как именно бедные и необразованные люди имели большие семьи и много детей, регламентация браков также считалась необходимостью.

Эти идеи буржуазное общество приняло воодушевленно, и уже в начале XX века сознательный отказ иметь больше допустимого числа детей среди всех семейных пар составил – 8%, в 50-х годах вырос — до 25%, а в 70—80-х составил – 45% [3].

В теории популяций уравнение Мальтуса называют уравнение

                                                                                                                   (1)

где ℰ = const, причем ℰ = b-m; b и m – коэффициенты рождаемости и смертности соответственно. Показатель  называют естественной скоростью роста популяций (мальтусовским коэффициентом прироста) [2].

Решением уравнения (1) является следующая функция

, где 

При  она определяет экспоненциальное увеличение численности популяции, а если , то численность стремится к 0 при . В случае, когда , численность популяции сохраняется на начальном уровне сколь угодно долго (рис. 1). Очевидно, для уравнения (1) значение параметра  является бифуркационным. При  уравнение (1) имеет одно положение равновесия , неустойчивое при  и асимитотически устойчивое при . Если уравнение (1) имеет бесконечно много положений равновесия вида , каждое из которых устойчиво, но не асимптотически [1].

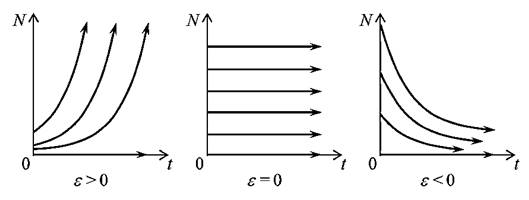
Рисунок 1. Геометрическая интерпретация решений Мальтуса

Интерпретируя решение уравнения (1), Мальтус утвердил, что в человеческом обществе существует абсолютный закон безграничного размножения особей [1]. И так как рост численности человеческого общества опережает темпы роста продовольственных запасов, то, следовательно, неизбежна жестокая конкуренция среди людей «за место под солнцем»: «Человек, появившийся на свет уже занятый другими людьми, если он не получил от родителей средств к существованию, если общество не нуждается в его труде, не имеет никакого права требовать для себя пропитания, ибо он совершенно лишний на этом свете. На великом пиршестве природы для него нет прибора. Природа приказывает ему удалиться, и если он не может прибегнуть к состраданию какого-либо из пирующих, она сама принимает меры к тому, чтобы ее приказание было произведено в исполнение» [2].

Сегодня, можно смело сказать, что выдвинутые еще в XVIII веке Томасом Мальтусом опасения о том, что рост численности населения всегда будет выше уровня экономического развития имеет место.

«Мальтузианский потолок» — понятие, введенное ученым относительно максимально допустимой численности населения нашей планеты к плодородным землям, имеющимся в распоряжении.

Если превысить «мальтузианский потолок», то неизбежно наступит голод и болезни, что приведет к «мальтузианской катастрофе», а именно высокая смертность вновь уравняет баланс природных ресурсов и населения.

Благодаря техническому прогрессу человек теперь меньше зависит от земли, что позволяет избегать катастрофы в мировом масштабе, но по-прежнему миллионы людей буквально выживают недоедая и существуя за чертой бедности.

Как и несколько веков назад повышение культурного и образовательного уровня среди бедных слоев, информированность и обеспечение контрацептивами могут помочь предотвратить «мальтузианскую катастрофу» [3].