ЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА ДЛЯ СЧЁТНЫХ СИСТЕМ ОДУ

LINEAR BOUNDARY VALUE PROBLEM FOR COUNTING SYSTEMS OF ODE

Madina Gazdieva

Student of Ingush State University, Russia, Magas

Ismail Tankiev

Scientific adviser, Сandidate of physical  and mathematical sciences, Head of the Department of Mathematical Analysis, Professor, Ingush State University, Russia, Magas

Аннотация. В данной статье рассматривается линейная краевая задача для счётных систем обыкновенных дифференциальных уравнений, а также сведение краевой задачи к системе интегральных уравнений. 

Abstract. This article considers a linear boundary value problem for countable systems of ordinary differential equations, as well as the reduction of the boundary value problem to a system of integral equations.

Ключевые слова: краевая задача, интегральные уравнения, счётные системы ОДУ, интегральные уравнения Вольтерра.

Keywords: boundary value problem, integral equations, counting systems of ODEs, Volterra integral equations.

Рассматривается счетная система обыкновенных дифференциальных уравнений

с краевыми условиями

где    ( j = 1, 2, …), а  - некоторые действительные числа, такие что

Функции  ( x,  будем предполагать определенными в области

Под решением задачи (1), (2) будем понимать непрерывные функции , удовлетворяющие системе     (1) и краевым условиям (2).

Вопросы непрерывности и ограниченности функций

рассмотрены в .

Будем предполагать, что правые части (1) :

1) непрерывны по совокупности переменных

( x, y ) = ( x, 

2)  причем

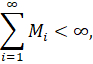
удовлетворяют условиям Липшица в области G :

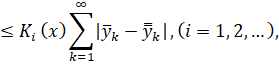
где  - некоторые непрерывные функции, определенные на  и такие, что

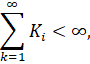
где

Займемся сведением задачи (1), (2) к системе интегральных уравнений.

Отметим, что в случае  задача (1), (2) превращается в краевую задачу для конечных систем ОДУ. Если же то имеем задачу КошиНиколетти для бесконечных систем. В случае   в (2) имеем линейную однородную краевую задачу [2].

Вместо системы (1) рассмотрим следующую систему интегральных уравнений:

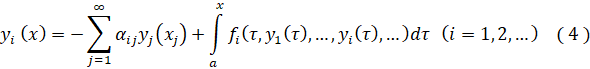
Нетрудно видеть, что задачи (1), (2) и (4) эквивалентны, причем каждое решение (4) удовлетворяет условиям (2).

Полагая в (4) последовательно x = решим полученную счетную систему линейных неоднородных алгебраических уравнений со счетным числом неизвестных  [3-5] вида

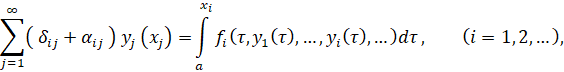
правые части которой есть ограниченные величины. символ Кронеккера.

Предполагая, что главный определитель этой системы

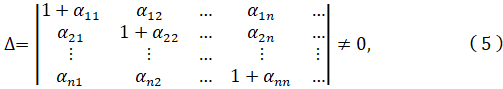
а  алгебраические дополнения s – го элемента  j - го столбца

Решая эту систему [1], находим 

Подставляя последние в (4), имеем счетную систему интегральных уравнений типа Вольтерра:

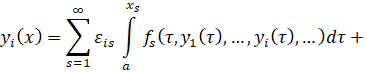
Здесь

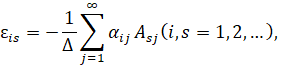
Причем

Нетрудно убедиться в эквивалентности задач (1), (2) и (6).