Многоточечная сингулярная краевая задача для систем обыкновенных дифференциальных уравнений
Секция: Физико-математические науки

XIX Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Многоточечная сингулярная краевая задача для систем обыкновенных дифференциальных уравнений
Рассматривается система
![]()
с краевыми условиями
![]()
где ![]() ;
;

правые части системы (1) заданы в области
![]()
![]() мерное вещественное евклидово пространство, а при
мерное вещественное евклидово пространство, а при ![]() они могут быть, вообще говоря, неограниченными. В этом случае задачу (1)
они могут быть, вообще говоря, неограниченными. В этом случае задачу (1)![]() (2) обычно называют сингулярной. В работах
(2) обычно называют сингулярной. В работах ![]() исследованы различные сингулярные краевые задачи. Насколько нам известно сингулярная задача (1)
исследованы различные сингулярные краевые задачи. Насколько нам известно сингулярная задача (1)![]() (2) не изучалась.
(2) не изучалась.
Введём обозначения: ![]() множество
множество ![]() -мерных вектор-функций с непрерывными на
-мерных вектор-функций с непрерывными на ![]() элементами:
элементами: ![]() множество
множество ![]() -мерных вектор-функций с абсолютно непрерывными на
-мерных вектор-функций с абсолютно непрерывными на ![]() элементами;
элементами; ![]() пространство суммируемых со степенью
пространство суммируемых со степенью ![]() на отрезке
на отрезке ![]() функций;
функций; ![]() множество
множество ![]() матриц, элементы которых принадлежат
матриц, элементы которых принадлежат ![]()
![]()
![]() множество функций определённых в области
множество функций определённых в области ![]() и удовлетворяющих локальным условиям Каратеодори;
и удовлетворяющих локальным условиям Каратеодори; ![]() множество
множество ![]() –мерных векторов, элементы которых принадлежат
–мерных векторов, элементы которых принадлежат![]()
![]() множество всех функций принадлежащих
множество всех функций принадлежащих ![]() для любого
для любого ![]() , если только
, если только ![]() ; аналогично вводится множество
; аналогично вводится множество ![]() .
.
Определение 1. Вектор-функция ![]() называется решением задачи (1),(2), если
называется решением задачи (1),(2), если ![]() удовлетворяет условиям (2) и почти всюду на
удовлетворяет условиям (2) и почти всюду на ![]() системе (1).
системе (1).
Определение 2. Будем говорить, что выполнено условие (А), если элементы матрицы ![]() таковы, что
таковы, что ![]()
![]()
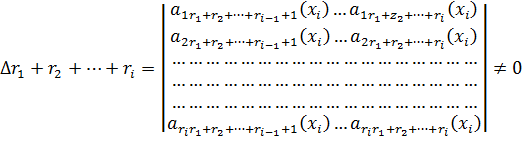
![]()

Рассмотрим систему дифференциальных уравнений
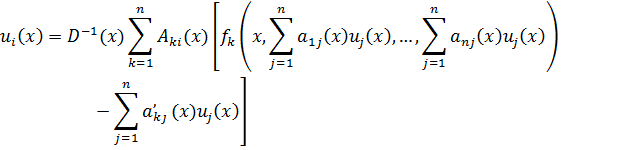
![]()
с краевыми условиями
![]()
где ![]() алгебраическое дополнение элемента
алгебраическое дополнение элемента ![]() определителя
определителя ![]() )
)
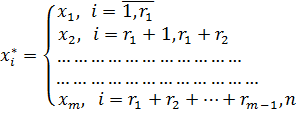
Теорема 1. Пусть задана матрица ![]() и выполнено условие
и выполнено условие ![]() , тогда задачи (1)
, тогда задачи (1)![]() (2) и (3)
(2) и (3)![]() (4) эквивалентны.
(4) эквивалентны.
Доказательство . Пусть задача (1)![]() (2) имеет решение
(2) имеет решение ![]()
Введём функции ![]() с помощью равенств:
с помощью равенств:

Из (5) имеем
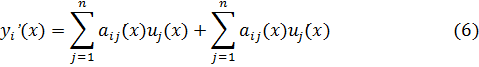
Подставляя (5),(6) в систему (1) получим


Решая (7) относительно ![]() получим (3): то есть функции
получим (3): то есть функции ![]() являются решением системы (3). Покажем, что
являются решением системы (3). Покажем, что ![]() удовлетворяет и условию (4).
удовлетворяет и условию (4).
Так как ![]() удовлетворяет условиям (2), то в силу условия
удовлетворяет условиям (2), то в силу условия ![]() имеют место равенства
имеют место равенства


![]()
![]()
![]()
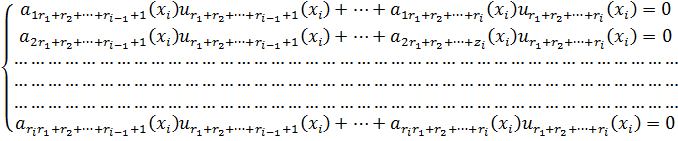
![]()
Отсюда


![]()
![]()

Следовательно имеет место равенство (4). Итак, функции ![]() являются решением задачи (3)
являются решением задачи (3)![]() (4).
(4).
Пусть функции ![]() являются решением задачи (3)
являются решением задачи (3)![]() (4). Тогда имеем тождество (3), из которых после умножения на
(4). Тогда имеем тождество (3), из которых после умножения на ![]() можно получить тождество (7) или
можно получить тождество (7) или

Следовательно функции (5) являются решением системы (1); из (5) и условия![]() следует, что они также удовлетворяют и условиям (2), что и требовалось.
следует, что они также удовлетворяют и условиям (2), что и требовалось.
Теорема 2. Пусть
![]()
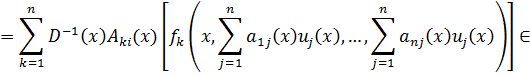
![]()
и в области
![]()
соблюдаются неравенства

![]()
![]() , где
, где ![]() неотрицательны, не убывают по внедиагональным элементам в области
неотрицательны, не убывают по внедиагональным элементам в области ![]() и для любого
и для любого ![]() найдётся такое положительное число
найдётся такое положительное число ![]() ,что
,что
![]()
какова бы ни была ![]() удовлетворяющая условиям
удовлетворяющая условиям
![]()
![]()
![]()
![]() неотрицательна и
неотрицательна и

если ![]()
Функции ![]() таковы, что имеет место условие
таковы, что имеет место условие ![]() . Тогда задача (1)
. Тогда задача (1)![]() (2) имеет хотя бы одно решение
(2) имеет хотя бы одно решение
![]()
Теорема 3. Пусть
![]() и в области соблюдаются неравенства
и в области соблюдаются неравенства
![]()
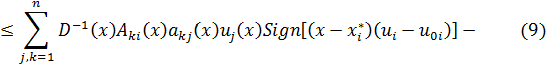
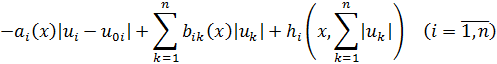
где функции ![]() таковы, что имеет место условие
таковы, что имеет место условие ![]() , где
, где ![]()
![]() ,
, ![]() и
и ![]() для каждого
для каждого ![]() удовлетворяют условиям теоремы 2; матрица
удовлетворяют условиям теоремы 2; матрица ![]() и система дифференциальных неравенств
и система дифференциальных неравенств
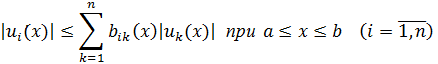
не имеет нетривиального решения ![]() удовлетворяющего условиям
удовлетворяющего условиям ![]() ; вектор-функция
; вектор-функция
![]() неотрицательна, не убывает по
неотрицательна, не убывает по ![]() в
в
![]() .
.
Тогда задача (1)![]() (2) имеет хотя бы одно решение
(2) имеет хотя бы одно решение ![]() . При этом, если
. При этом, если ![]() и
и ![]() не удовлетворяют указанным условиям, то найдётся удовлетворяющая условиям (3) вектора
не удовлетворяют указанным условиям, то найдётся удовлетворяющая условиям (3) вектора![]() функция
функция ![]() для которой задача (1)
для которой задача (1)![]() (2) не имеет решения.
(2) не имеет решения.
Следствие 1. Пусть
![]()
и в области ![]() соблюдаются неравенства (9), где
соблюдаются неравенства (9), где ![]()
![]() ,
, ![]() ,
, ![]() и
и ![]() удовлетворяют условиям теоремы 2, а
удовлетворяют условиям теоремы 2, а ![]() условиям теоремы 3.
условиям теоремы 3.
Тогда задача (1)![]() (2) имеет хотя бы одно решение
(2) имеет хотя бы одно решение ![]() , если только матрица
, если только матрица ![]() неотрицательна и удовлетворяет одному из следующих трёх условий:
неотрицательна и удовлетворяет одному из следующих трёх условий:
1. ![]() и
и
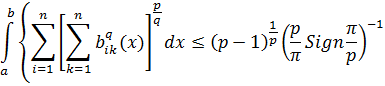
![]()
![]() .
.
2. ![]() постоянная матрица и все её собственные числа по модулю меньше чем
постоянная матрица и все её собственные числа по модулю меньше чем ![]()
3. ![]() и
и

![]()
![]() и все собственные числа матрицы
и все собственные числа матрицы ![]() по модулю меньше единицы.
по модулю меньше единицы.
Следствие 2. Пусть
![]()
и в области ![]() соблюдаются неравенства
соблюдаются неравенства
![]()
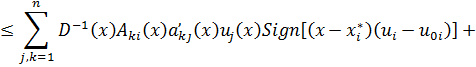

где ![]() удовлетворяют условиям (А),
удовлетворяют условиям (А), ![]() неотрицательная постоянная матрица,
неотрицательная постоянная матрица, ![]() и
и ![]()
![]() . Пусть, кроме того, найдётся такое неотрицательное число
. Пусть, кроме того, найдётся такое неотрицательное число ![]() , что
, что

и все собственные числа матрицы ![]() по модулю меньше, чем
по модулю меньше, чем ![]() . Тогда задача (1)
. Тогда задача (1)![]() (2) имеет хотя бы одно решение (которое, вообще говоря, не является абсолютно непрерывным на
(2) имеет хотя бы одно решение (которое, вообще говоря, не является абсолютно непрерывным на ![]() .
.
Теорема 4. Пусть
![]()
и в области ![]() соблюдаются неравенства
соблюдаются неравенства
![]()

![]()
![]()

![]()
![]()
где ![]()
![]() удовлетворяют условию (А),
удовлетворяют условию (А), ![]() и
и ![]() для каждого
для каждого ![]() удовлетворяют условиям теоремы 2,
удовлетворяют условиям теоремы 2, ![]()
![]() а
а ![]()
![]() непрерывные и положительные в
непрерывные и положительные в ![]() функции, удовлетворяющие условиям
функции, удовлетворяющие условиям

Тогда задача (1)![]() (2) имеет хотя бы одно решение
(2) имеет хотя бы одно решение
![]()
Теорема 5. Пусть при ![]() соблюдаются неравенства
соблюдаются неравенства
![]()
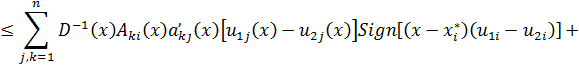

где ![]() удовлетворяют условиям (А),
удовлетворяют условиям (А), ![]() , удовлетворяет условиям теоремы 3. Тогда задача (1)
, удовлетворяет условиям теоремы 3. Тогда задача (1)![]() (2) имеет не более одного решения.
(2) имеет не более одного решения.
Следствие 1. Если при ![]() соблюдаются неравенства (10), где
соблюдаются неравенства (10), где ![]() удовлетворяют (А), а матрица
удовлетворяют (А), а матрица ![]() одному из условий 1), 2), 3) следствия 1 теоремы 3, то задача (1)
одному из условий 1), 2), 3) следствия 1 теоремы 3, то задача (1)![]() (2) имеет не более одного решения.
(2) имеет не более одного решения.
Следствие 2. Если при ![]() соблюдаются неравенства
соблюдаются неравенства
![]()


где ![]() удовлетворяют условиям (А),
удовлетворяют условиям (А), ![]() и
и ![]()
![]() условиям следствия 2 теоремы 3, то задача (1)
условиям следствия 2 теоремы 3, то задача (1)![]() (2) имеет не более одного решения.
(2) имеет не более одного решения.
Доказательство теорем 2-5 и следствий 1-2 вытекает из теоремы 1 с учётом результатов работы [ 2 ].





