Использование распределения Гаусса для выявления кратковременных спадов FPS

Неотъемлемой частью жизни молодого поколения несомненно являются видеоигры. Это подтверждается не только широкой распространенностью культуры видеоигр в мире, но и признанием киберспортивных дисциплин официальным видом спорта в разных странах (Россия стала первой страной в мире, которая признала киберспорт официальным видом спорта. Это произошло 25 июля 2001 года по распоряжению тогдашнего главы Госкомспорта России Рожкова Павла Алексеевича). Для проведения соревнований, необходимо обеспечить комфортную производительность вычислительных машин, на которых спортсмены принимают участие в игре. Исходя из вышеизложенного, нужно понять, каким образом определять комфорт игры. При решении этой проблемы было придумано несколько методов, один из которых – вычисление показателя 1% минимального FPS и сравнение его со средним значением FPS.

FPS (англ. Frames Per Second - кадры в секунду) – количество кадров, показанных за одну секунду. В большинстве случаев график зависимости значения FPS(с^-1) от времени t(c) используется для определения комфортности игры. И в случае, если в какой-то момент времени происходит кратковременный спад (просадка) FPS, то такой спад легко увидеть на графике.

Рисунок 1. Пример просадок FPS

Но есть случаи, когда просадки бывают в промежутке, меньшем чем одна секунда. Такие моменты не фиксируются графиком зависимости FPS от времени, т.к. время на графике описывается целым числом секунд. Эквивалентом средней производительности за определенный промежуток времени является среднее значение времени кадра в этом промежутке. Допустим, необходимо узнать среднее значение времени кадра среди десяти показанных кадров.

Таблица 1.

Показатели

Расчёт среднего значения времени кадра:

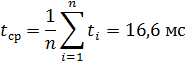
Хороший результат: среднее значение времени получилось эквивалентом 60 FPS. Но, к сожалению, это не показывает полной картины. Если взглянуть на таблицу, можно увидеть, что результат на 2 и 5 кадре сильно выше среднего результата. Не исключены похожие просадки и во время длительной игры, они могут быть реже, но все-таки они неприятны и сильно мешают игровому процессу, а в напряженные моменты они могут стать причиной поражения киберспортивной команды. Для выявления таких просадок было решено использовать распределение Гаусса.

Распределение Гаусса (нормальное распределение, распределение Гаусса-Лапласа) – распределение вероятностей, которое в одномерном случае задается функцией плотности вероятностей, совпадающей с функцией Гаусса:

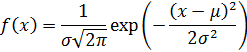
где  – математическое ожидание,  – среднеквадратичное отклонение распределения,  – дисперсия распределения.

Как уже было отмечено, среднее значение времени кадра не показывает редкие просадки. Для того, чтобы определить, что игроку использовать данную вычислительную машину будет комфортно, нужно построить график распределения Гаусса, а затем вычислить так называемый показатель 1% минимального FPS (англ. – 1% min FPS, или реже – 1% low).

Чтобы получить значение 1% минимального FPS, сначала вычисляется время кадра, вероятность появления которого равна 0,01. После этого, среди кадров, больших полученного значения вычисляется среднее время, а затем рассчитывается соответствующий этому показателю FPS.

Для построения графика был проведен эксперимент, в котором на персональном компьютере была запущена одна из киберспортивных дисциплин. В результате эксперимента было получено n=4096 измерений времени кадра, рассчитаны значения:

По рассчитанным значениям построен график нормального распределения:

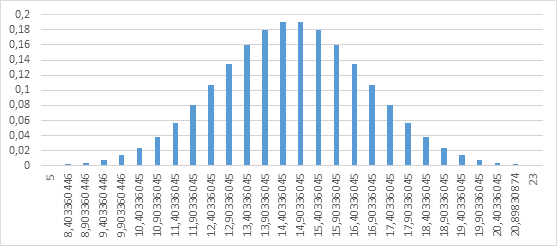
Рисунок 2. Нормальное распределение времени кадра. По горизонтали – время кадра(мс), по вертикали – плотность вероятности

Теперь, среди всех измерений нужно вычислить показатель 1% минимального FPS. В следствие того, что необходимо выявить задержки, т.е. кадры с большим временем, необходимо рассматривать область графика, расположенную правее математического ожидания. Следующим шагом вычисляется время кадра, вероятность появления которого равна 0,01, таким временем является 19,496 мс. Далее, среди реальных значений берутся те, что больше 19,496 мс и среди них вычисляется среднее время кадра, в данном случае оно равно 33,437 мс, это соответствует значению FPS равному 30. Следовательно, показатель 1% минимального FPS равен 30.

Можно сделать вывод, что среди полученных измерений времени кадра кратковременное падение частоты кадров происходит с 68 FPS до 30 FPS. Это серьезная просадка, не приемлемая во время соревнований. Однако для рядового игрока-любителя она не критична.

Таким образом, удалось выявить редкие скачки времени кадра, не фиксируемые графиком среднего FPS, используя распределение Гаусса. Такой способ в последнее время все чаще применяется в тестировании вычислительных машин. Интегрирование этого метода в программное обеспечение компьютера поможет избежать неприятных просадок и достичь максимального комфорта игры.