Действия групп на множествах. Лемма Бернсайда. Задача об ожерельях и ее практическое применение в кодировании информации

В современном стремительно развивающемся мире высоких технологий особую значимость приобретают  математические разделы, имеющие отношение к развитию ЭВМ. Одним из таких разделов является алгебраические структуры. Это связано с тем, что с помощью групп можно легко описать огромное количество различных объектов и ситуаций с ними. Именно поэтому исследование алгебраических структур не утрачивает своей актуальности в разработке различных оптимизационных алгоритмов.

Цель работы: В данной статье необходимо рассмотреть алгоритм решения задачи об ожерельях, а также её практическое применение в области кодирования информации.

Определение 1. Пусть G — группа, Ω — множество. Говорим, что определено действие группы G на множестве Ω, если определено отображение G × Ω → Ω (т. е. для любых g ∈ G, ω ∈ Ω определён g(ω) ∈ Ω), удовлетворяющее следующим свойствам: 1. (gh)(ω) = g(h(ω)) 2. e(ω) = ω 

Определение 2. Действие группы G на множество Ω — это гомоморфизм G → S(Ω), где S(Ω) — группа всех биекций множества Ω в себя. 

Утверждение . Данные определения эквивалентны.

Задача. Какое количество ∃ различных ожерелий, составленных из n желтые и m зеленые бусины? (Считается, что 2 ожерелья совпадают, если одно можно заполучить из другого путем поворота.)

Выполнение этой задачи осуществляется с помощью леммы Бернсайда, позволяющей получить и множество других результатов.

Сначала немного истории. Уильям Бернсайд (1852–1927) привел доказательство этой леммы в своей книге в 1897 г. Однако выяснилось, что данную формулу знали еще Коши (1845 г.) и Фробениус (1887 г.). Видимо, лемма была настолько хорошо известна, что Бернсайд не указал авторство Коши. Данный результат имеет несколько названий (кроме уже приведенного): лемма Коши — Фробениуса, лемма не Бернсайда (в области теории групп очень многие результаты принадлежат именно Бернсайду).

Для формулировки леммы понадобятся некоторые сведения. Поскольку нам интересна задача об ожерельях, на ее решении будем все рассматривать.

Обозначим через M множество всех ожерелий. Пусть G — множество всех различных поворотов ожерелий (ясно, что разных поворотов всего n + m). Очевидно, что G — группа. При этом каждому ожерелью из M можно сопоставить ожерелье, полученное из него с помощью поворота g∈ G. При этом два ожерелья считаются одинаковыми, или эквивалентными, если одно можно перевести в другое каким-либо поворотом из G. Таким образом, все ожерелья разбиваются на классы эквивалентности, или орбиты. Наша задача — найти число различных орбит.

Теперь рассмотрим какой-либо поворот ожерелья. Назовем данный вариант ожерелья неподвижной точкой относительно данного поворота, если после применения этого поворота ожерелье останется прежним в формально (на каждом месте будет находиться бусина того же самого цвета). Обозначим через I(g) количество неподвижных точек поворота g.

Лемма Бернсайда. Количество орбит равно сумме количеств неподвижных точек по всем элементам группы G, деленной на мощность этой группы:

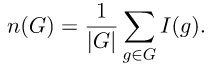
Доказательство леммы Бернсайда (Bogart, Kenneth, 1991).

Очевидно, что

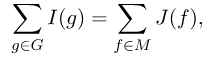
где f— фиксированный элемент множества M, а J(f) — число различных элементов G, которые переводят f в себя (относительно которых f инвариантен).

Составим таблицу следующим образом. Каждый столбец будет соответствовать одному элементу множества m ∈ M, каждая строка — элементу g ∈ G. В данном столбце и данной строке стоит элемент из M, в который переходит элемент, соответствующий данному столбцу, при применении к нему элемента из G, соответствующему данной строке.

Задача об ожерельях и ее практическое применение в кодировании информации.

Перейдем к главной теме вопроса, как связаны задача об ожерельях и проблемы кодирования. Когда отправляются кодированные сообщения соблюдается определенная синхронность работы передающих и принимающих сторон каналов связи.

Для синхронизации каналы обеспечиваются дополнительными устройствами - тактовыми генераторами. Если генераторы дают сбой, то в кодовом слове за начальный символ выбирается символ, не являющийся начальным.

Следовательно построение кодов, которые могут восстановить синхронизацию, будет всегда актуально. 

Возможный путь решения данной проблемы (Не считая исправлений ошибок символов) состоит в следующем: рассмотрим множество n-буквенных кодовых слов, удовлетворяющих такому ограничению: если (a1, a2,... an,) и (b1, b2...bn,) - кодовые слова, то никакие из их пересечений (a1a3,...anb1,), (a3..anb1b2), (anb1...bn-1) не будут кодовыми словами.

Данные коды называются синхронизируемыми, и они, способны восстановить синхронизацию. К несчастью, существует проблема: при улучшении кода уменьшается число кодовых слов. Но так ли велика эта проблема? Чтобы ответить на этот вопрос используем решение задачи об ожерельях.

И правда, если а= (a1, a2, a3... an) - кодовое слово синхронизируемого кода, следовательно кодовым словом его циклический сдвиг не является, потому что он будет пересечением для пары (а, а). Так же, из-за этого любое кодовое слово обязано быть основным.

Поэтому наибольшее число n-буквенных слов синхронизируемого кода, который использует алфавит из m символов, не превосходит числа несоставных ожерелий с n бусинками из m разных цветов.

Обозначив данное число в виде Wn(m), получаем 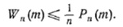. В итоге, используя (1), мы получаем верхнюю границу числа n-буквенных кодовых слов для синхронизируемого кода: 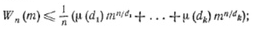(2) (здесь di...dk, по-прежнему все разные делители n).

Заключение:  Таким образом, в данной работе мы достигли своей цели, представив практическое применения решения конкретной задачи об ожерельях в лице синхронизируемых кодов, а также рассмотрели алгоритм решения с помощью леммы Бернсайда.