Оптическая рефракция в земной атмосфере

Пространственно-временная изменчивость свойств атмосферы создает большие трудности при определении и прогнозировании рефракционных искажений. Поэтому при рассмотрении проблемы рефракции необходимо дать основные сведения о строении и составе атмосферы в соответствии с современными представлениями.

Строение земной атмосферы

Земная атмосфера по физическим свойствам неоднородна и по вертикали, и по горизонтали. Приведем современную классификацию деления атмосферы на слои, а также рассмотрим горизонтальное строение атмосферы.

Вертикальное строение атмосферы. В наибольшей степени атмосфера неоднородна по высоте, ввиду чего ее обычно подразделяют на несколько слоев. При вертикальной протяженности атмосферы, достигающей 60-70 тыс. км (резкой верхней границы не существует – атмосфера постепенно переходит в межпланетную среду), 99 % всей ее массы сосредоточено в слое высотой 30-35 км, что и определяет ее основную роль в различных физических процессах.

Рассмотрим плоскую монохроматическую волну вида

      (2.1)

где   и   – амплитудная и фазовая функции от координат; k= 2;   – длина волны в вакууме.

Для подобных волн возможен переход от волновой оптики к геометрической при распространении и в неоднородных средах (например, в атмосфере).

Характеризуя оптические свойства среды коэффициентом преломления n, являющимся также функцией от координат, запишем уравнение монохроматической волны

        (2.2)

Решение (2.2) будем искать в виде (2.1). Найдя производные от   по всем координатам и подставляя полученные значения, а также (2.1) и (2.2), получим:

       (2.3)

В связи с тем, что для оптического диапазона длина волн    (следовательно, k очень велико), второй и третий члены (2.3) пренебрежительно малы по сравнению в первым, т.е. можно записать:

(2.4)

Или

       (2.5)

Функция   является решением (2.5) для любого и    представляет собой поверхность разных фаз и называется эйконалом, а уравнение (2.5) – уравнение эйконала. Поверхности, где эйконал не изменяется, называется волновыми фронтами, а траектории, ортогональные к ним, - лучами.

Умножая обе части уравнения (2.4) на единичный вектор   и применяя к нему операцию rot, можно получить

             (2.6)

Откуда следует, что интеграл по любому замкнутому контуру от   равен нулю.

·        Закон преломления

            (2.7)

·        Закон отражения

            (2.8)

Для получения уравнения лучей в такой среде уравнение эйконала запишем в виде

              (2.9)

Где   – радиус-вектор произвольной точки луча, а s – длина луча, отсчитываемая от этой точки. Вдоль каждого луча, лежащего в плоскости, проходящей через начало координат, выполняется условие

           (2.10)

Где   – угол между векторами    и   .

В диэлектрической среде (таковой является атмосферный воздух) плоская волна распространяется со скоростью

               (2.11)

где  — скорость света в вакууме;  — диэлектрическая и магнитная проницаемости, характеризующие взаимодействие излучения со средой.

Исходя и этого, коэффициент преломления определяется формулой

               (2.12)

при сравнении которой с (2.11) получаем известное выражение Максвелла:

                   (2.13)

Также используется формула Эдлена для расчета  в зависимости от :

(2.14)

Для атмосферного воздуха коэффициент преломления пропорционален плотности воздуха. Это позволяет с большой точностью записать следующую зависимость  от давления P и температуры T воздуха:

                   (2.15)

в которой  – коэффициент преломления при стандартных условиях (, ).

Расчет Расчет угла астрономической рефракции производим по строгой формуле:

где  –  угол между нормалью к изодиоптрической поверхности (поверхности одинакового коэффициента преломления) и направлением оптического луча;

n – коэффициент преломления, связанный с индексом преломления N выражением

 – индексы преломления в начальной среде G и конечной A точках траектории оптического луча.

Верхний предел интегрирования при расчете астрономической рефракции равен . Интегрирование выполняется для сферической модели атмосферы численным методом по формуле парабол, приведенной в /1,2/ для общего случая, когда узлы интегрирования располагаются в произвольных точках пути оптического луча. После численного интегрирования

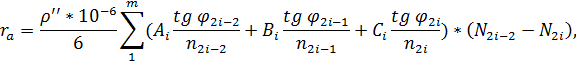
где

Индекс преломления в начальной точке

                (4.1)

где  – индексы преломления и абсолютные температуры на нижней границе.

подставляем в (4.1)

Для сферической модели атмосферы угол  между нормалью к изодиоптрическим поверхностям и направлением оптического луча соответствует зенитному расстоянию, определенному по известной формуле:

                  (4.2)

где  - радиусы кривизны сферической изодиоптрической поверхности в текущей и начальной точках, в которых коэффициент преломления воздуха равен  и  соответственно.

Из (4.2) имеем

где  – геометрическая высота текущей точки относительно начальной.