ИССЛЕДОВАНИЕ МИКРОТВЕРДОСТИ ОБРАЗЦОВ МАГНИЯ В УСЛОВИЯХ ЭЛЕКТРОПЛАСТИЧНОСТИ
Конференция: CCLXXVII Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Физико-математические науки

CCLXXVII Студенческая международная научно-практическая конференция «Молодежный научный форум»
ИССЛЕДОВАНИЕ МИКРОТВЕРДОСТИ ОБРАЗЦОВ МАГНИЯ В УСЛОВИЯХ ЭЛЕКТРОПЛАСТИЧНОСТИ
Измерение микротвердости относится к микромеханическим испытаниям, которые были разработаны для металлографических исследований свойств отдельных структурных составляющих сплавов.
Метод измерения микротвердости при металлографических исследованиях во многих случаях позволяет получить результаты, недостижимые при макроскопических механических испытаниях. Например, измерения микротвердости и участков с мартенситной структурой, возникших на месте зерен перлита в стали после действия световых импульсов лазера, показали, что их твердость почти в полтора раза выше, чем твердость стали после обычной закалки в воде. Этот эффект, имеющий большое научное и практическое значение, связан с тем, что нагрев и охлаждение металла при лазерной обработке происходит со скоростями в тысячи раз большими, чем при обычной закалке.
Измерение микротвердости производят по методу восстановленного отпечатка (основной) или по методу невосстановленного отпечатка (дополнительный) с использованием:
- четырехгранной пирамиды с квадратным основанием:
- трехгранной пирамиды с основанием в виде равностороннего треугольника:
- четырехгранной пирамиды с ромбическим основанием:
- бицилиндрического наконечника.
Для измерения микротвердости фазовых структурных составляющих и для получения распределения микротвёрдости по толщине химико-термически обработанных слоев применяют микротвердомер ПМТ-3 и программное обеспечение для него Altami Studio 3.4.
Для определения глубины отпечатка воспользуемся формулой 2.1:
![]() (2.1)
(2.1)
где:
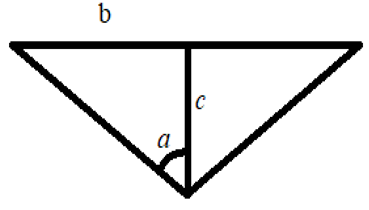
![]()
Рисунок 2.1. Треугольник для определения глубины отпечатка
Таблица 2.1.
Измерения глубины отпечатка в зависимости от нагрузки Р и времени инденсирования t.
|
Нагрузка, Р |
Время, с |
Микротвердость, HV (Глубина отпечатка, мкм) |
|
|
Образец без тока |
Образец с током |
||
|
50 |
5 |
177,4 (9,235) |
190,0 (9,373) |
|
8 |
171,8 (9,490) |
166,2 (9,708) |
|
|
10 |
238,7 (8,177) |
258,0 (7,869) |
|
|
15 |
159,9 (9,248) |
165,0 (10,783) |
|
|
20 |
151,6 (9,829) |
153,2 (9,995) |
|
|
100 |
5 |
164,4 (13,292) |
255,2 (11,029) |
|
8 |
182,8 (13,611) |
192,2 (12,286) |
|
|
10 |
193,0 (12,726) |
216,0 (12,548) |
|
|
15 |
164,0 (12,819) |
212,0 (11,975) |
|
|
20 |
157,0 (13,558) |
192,0 (12,989) |
|
|
200 |
5 |
192,8 (18,624) |
199,2 (20,818) |
|
8 |
195,6 (18,160) |
173,0 (18,277) |
|
|
10 |
209,9 (17,796) |
198,9 (18,140) |
|
|
15 |
199,3 (17,368) |
220,0 (17,142) |
|
|
20 |
185,1 (17,736) |
189,2 (18,083) |
|
|
300 |
5 |
173,5 (22,252) |
194,9 (22,192) |
|
8 |
179,7 (23,004) |
182,0 (22,729) |
|
|
10 |
179,5 (22,442) |
165,1 (23,707) |
|
|
15 |
163,7 (23,347) |
151,9 (25,492) |
|
|
20 |
167,3 (23,452) |
165,8 (23,262) |
|
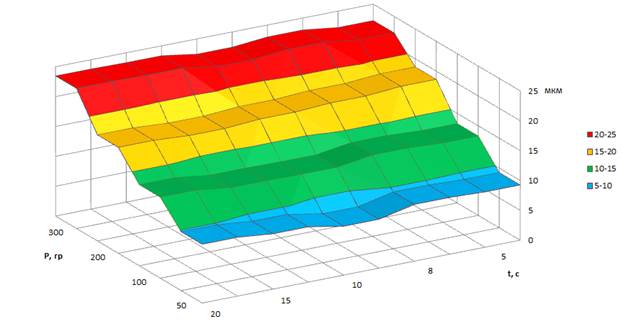
Рисунок 2.2. Глубина отпечатка образца магния с плотностью тока j=0 А/мм2
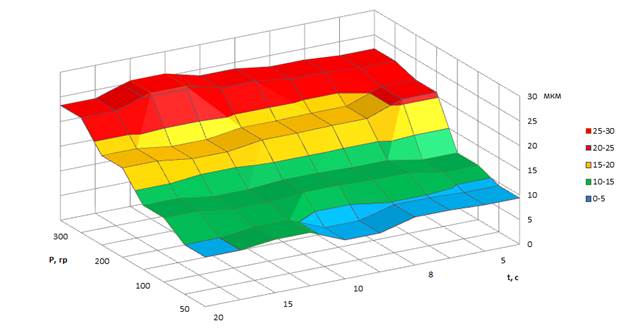
Рисунок 2.3. Глубина отпечатка образца магния с плотностью тока j=103 А/мм2 и длительностью t=10-4 с.
Из приведенных графиков наглядно видна зависимость величины нагрузки на глубину отпечатка: чем выше нагрузка, тем глубже получается отпечаток. Это наблюдается как в образце без тока, так и в образце с током.
3 Измерение гистерезисных потерь при локальном контактном деформировании материалов
Одним из наиболее распространенных случаев силового взаимодействия деталей машин и конструкций является контактное нагружение, которое возникает в процессе совместной работы сопряженных элементов. Сопротивление материала упругопластической контактной деформации является одним из важнейших факторов, определяющих условия трения и износа деталей машин, контактную жесткость элементов машиностроительных конструкций, их прочность и эксплуатационную надежность, предпочтительные режимы поверхностной упрочняющей обкатки деталей и т. д. В результате усталости при циклическом нагружении происходит значительная часть отказов машин. Под действием циклических нагрузок II материале происходят процессы постепенного накопления повреждений, приводящие к изменению его свойств, образованию трещин и в итоге к полному разрушению детали или образца. Опасность заключается в том, что они могут протекать под действием напряжений, намного меньших пределов прочности и текучести, в течение длительного времени и затем заканчиваться быстрым разрушением. В связи с этим важной задачей является разработка эффективных методик и критериев для количественной оценки способности материала работать в условиях контактного циклического нагружения без разрушения.
Одним из параметров материала, характеризующим его структуру и стойкость к усталостному разрушению, является величина обратимой неупругой (релаксационной) деформации при повторных нагружениях.
Обратимую неупругую деформацию можно найти из общую деформацию:
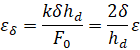
где ![]() – эффективная деформация (
– эффективная деформация (![]() )
)
![]() – глубина отпечатка, мкм;
– глубина отпечатка, мкм;
![]() – величина проекции отпечатка;
– величина проекции отпечатка;
![]() – величина общей деформации.
– величина общей деформации.
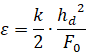
где ![]() – коэффициент, зависящий от типа индентора (для пирамиды
– коэффициент, зависящий от типа индентора (для пирамиды ![]() );
);
В свою очередь еще одним важным показателем является упругая деформация, которая также может возникать в материалах. Она рассчитывается по следующей формуле:
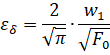
де ![]() – величина упругого сближения, она рассчитывается по формуле:
– величина упругого сближения, она рассчитывается по формуле:
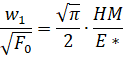
где ![]() - постоянные значения физико-механических свойств материала.
- постоянные значения физико-механических свойств материала.
Отсюда рассчитываем упругую деформацию для разных нагрузок, получаем:
нагрузка 50, время 10с - ![]() ;
;
нагрузка 100, время 50с - ![]() ;
;
нагрузка 300, время 20с - ![]() .
.
Посчитав значения упругой деформации, получили, что они не отличаются друг от друга, что свидетельствует об отсутствии упругой деформации.
Упругой деформацией называют деформацию, влияние которой на форму, структуру и свойства тела устраняется после прекращения действий внешних сил. Под действием нагрузки происходит незначительное обратимое смещение атомов. При смещении атомов из положения равновесия нарушается баланс сил притяжения и отталкивания, поэтому после снятия нагрузки атомы возвращаются в исходное положение, приобретают свою первоначальную форму. В данном случае, отсутствие пластической деформации говорит нам о том, что при нагрузке на образец кристаллическая решетка разрушается, при этом межатомная связь становиться крайне мала либо отсутствует в целом, что не позволяет атомам возвращаться к исходному положению и форме.
Заключение
Полученные результаты показали, что в результате воздействия импульсов тока микроструктура образца измельчается, что приводит к улучшению прочностных характеристик материала, микротвердость образца, подвергшего воздействию импульсов тока увеличилась.
Гистерезисные потери при локальном контактном деформировании материалов показали, что значения упругой деформации при различных нагрузках не отличаются друг от друга, а это свидетельствует об отсутствии упругой деформации.





