Представление булевых функций в СДНФ и её программная реализация

В курсе дискретной математики изучаются функции, область определения которых – дискретное множество. Простейшим (но нетривиальным) таким множеством является множество, состоящее из двух элементов. Цель статьи – написание программы построения СДНФ для функций алгебры логики на языке высокого уровня С++.

Булева функция (или логическая функция, или функция алгебры логики) от n аргументов — в дискретной математике – это отображение B_n → B, где B = {0,1} – булево множество.

Арность функции алгебры логики – это количество её аргументов.

Каждая булева функция арности n полностью определяется своими значениями на своей области определения, то есть на всех булевых векторах длины n. Число таких векторов равно 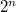. Поскольку на каждом векторе булева функция может принимать значение либо 0, либо 1, то количество всех n-арных булевых функций равно .

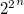ДНФ (Дизъюнктивная Нормальная Форма) — нормальная форма, где булева функция имеет вид дизъюнкции нескольких простых конъюнктов.

СДНФ (Совершенная Дизъюнктивная Нормальная Форма) – это такая ДНФ, которая удовлетворяет условиям:

·     в ней нет одинаковых простых конъюнкций;

·     каждая простая конъюнкция полная (если в неё каждая переменная (или её отрицание) входит только 1 раз).

Теорема.

Если булева функция не равна тождественному нулю, то ее можно представить в виде СДНФ по ее таблице истинности следующим образом: берем только те наборы переменных (х₁,х₂, …,х_n), для которых f(х₁,х₂, …,х_n) =1, и составляем простую конъюнкцию для этого набора так: если хi = 0, то берем в этой конъюнкции отрицание x_i, если х_i = 1, то берем х_i. Составляя дизъюнкцию этих простых конъюнкций, придем к СДНФ.

Пример построения СДНФ.

Таблица 1.

Таблица истинности со значениями функции от трех переменных

Тогда СДНФ:

F(x, y, z )= -x-yz v –xy-z v xyz

Программная реализация СДНФ.

Для написания программы, воспользуемся следующим алгоритмом:

1.  Создаём динамическую матрицу для таблицы истинности произвольного размера (размер задаём сами), и значениями функции.

2.  Находим строки, где значение функции принимает 1.

3.  Выпишем для этой строки конъюнкцию всех переменных: если значение переменной в данной строке равно 1, то в конъюнкцию включаем саму переменную, если 0, то включаем отрицание этой переменной.

4.  Все полученные конъюнкции свяжем в дизъюнкцию.

Код программы:

#include <iostream>

#include <locale.h>

using namespace std;

int main()

{

int n,m,i,j,k=0; float **bul; int *p;

setlocale( LC_ALL,"Russian" );

cout<<"Введите m, n и таблицу истинности из расчета n=2^m, где n-столбцы, m-строки."<< endl;

cout<<"m="; cin>>m; cout<<"n="; cin>>n;

m=m+1;

bul=new float *[n];

for(i=0;i<n;i++)

bul[i]=new float(m);

p=new int[m];

cout<<"Ввод таблицы, где последний столбец значение функции:"<<endl;

for(j=0;j<m-1;j++)

{ cout<<"X"<<j+1<<" ";}

for(j=m-1;j<m;j++)

cout<<"F "<<endl;

for(i=0;i<n;i++)

for(j=0;j<m;j++)

cin>>bul[i][j];

cout<<"СДНФ для этой функции:\n "<<endl;

for(i=0;i<n;i++)

{ if (bul[i][m-1]==1)

{ for(j=0;j<m-1;j++)

if(bul[i][j]==0)

{ cout<<"-X"<<j+1;}

else

cout<<"X"<<j+1;

if (i<n-1)

cout<<" v "; }

}

cout<< endl;

for(i=0;i<n;i++)

delete [ ] bul[i]; delete [ ] bul;

return 0;

}

Тестирование программы:

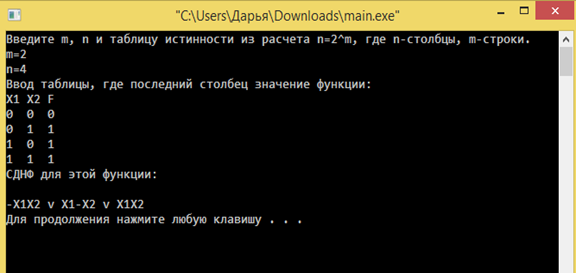
Рисунок 1. СДНФ для ФАЛ от двух переменных

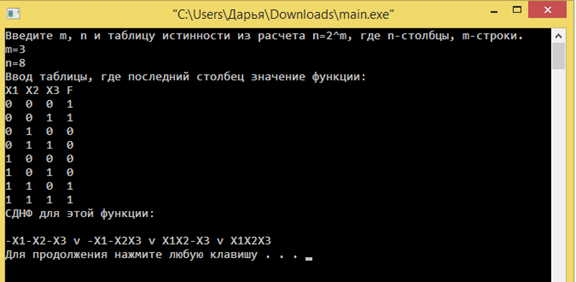
Рисунок 2. СДНФ для ФАЛ от двух переменных