РЕГРЕССИОННЫЙ МЕТОД В ИНФОКОММУНИКАЦИОННОЙ ТЕХНОЛОГИИ ПРИ ИССЛЕДОВАНИИ ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ СПУТНИКОВЫХ ДАННЫХ
Секция: Физико-математические науки

LXXIII Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
РЕГРЕССИОННЫЙ МЕТОД В ИНФОКОММУНИКАЦИОННОЙ ТЕХНОЛОГИИ ПРИ ИССЛЕДОВАНИИ ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ СПУТНИКОВЫХ ДАННЫХ
Из года в год на всей территории земного шара преобладает проблема лесных пожаров, неконтролируемого стихийного бедствия, пагубно отражающегося на экономике республики в целом и лесном комплексе в частности. Для решения такой масштабной задачи необходимо использовать различные средства и методы системы раннего обнаружения лесных пожаров.
Одним из методов анализа данных является регрессионный анализ, который позволяет определить связь между зависимой переменной и набором независимых, и использовать эту связь для прогнозирования значений.
Наиболее распространённый вид регрессионного анализа — линейная регрессия, когда находят линейную функцию, которая, согласно определённым математическим критериям, наиболее соответствует данным. Например, в методе наименьших квадратов вычисляется прямая (или гиперплоскость), сумма квадратов между которой и данными минимальна.
Математическое определение регрессии можно определить следующим образом. Пусть Y - зависимая переменная, а x1, x2,….. xn независимые переменные (факторы), определяющие поведение зависимой переменной. При построении модели, описывающей зависимость Y от x1, x2,….. xn , предполагается, во-первых, что у исследователя имеются результаты совокупных наблюдений зависимой переменной Y и независимых переменных x1, x2,….. xn , во-вторых, что значения независимых переменных определяются точно (без ошибок), а значение зависимой переменной Y определяется с ошибками, имеющими случайный характер. Математическая модель, описывающая данные такого вида, выглядит следующим образом:
![]()
где: ε - случайная ошибка наблюдений зависимой переменной.
Таким образом, регрессия описывает поведение наблюдаемой зависимой переменной в среднем, представляя ее главную тенденцию. В связи с этим нахождение регрессии по результатам наблюдений называют сглаживанием данных.
Исходя из географических особенностей исследуемой территории общая площадь лесного фонда составляет 90% от всей площади территории. Из них сосна занимает большую часть – 41 %.
По проведенному анализу статистических данных, взятых из ГИС было выявлено, что на территории одного муниципального образовании за последние 5 лет произошло наибольшее количество возгораний. Анализ горимости лесов показал, что одной из основных причин возникновения пожаров, являлось неосторожное обращение с огнем местного населения. Возникновению пожаров способствует не только человеческий фактор, но и такие как климат, погода, влияющая на созревание лесных горючих материалов (ЛГМ), пирологические характеристики растительности, антропогенное воздействие [1, 2, 3].
В случае системы раннего обнаружения лесных пожаров, зависимой переменной может быть вероятность возникновения пожара, а независимыми переменными – метеорологические показатели. Для построения регрессионной модели использовась статистические данные о значениях этих переменных в периоды, когда происходили пожары. Такая модель будет полезна для предсказания вероятности возникновения пожара на основе текущих значений переменных, а также для своевременного (оперативного) принятия мер по борьбе с возгораниями.
Так как в модели используется несколько факторов влияющих на количество возгораний, то будем применять множественную линейную регрессию.
Формула множественной линейной регрессии имеет вид:
Y = R0 + R1 *X1 + R2 * X2+….. Rn * Xn
где: Y – количество возгораний (термические точки);
X1 - температура воздуха (градусы Цельсия) на высоте 2 метра над поверхностью земли;
X2 - скорость ветра на высоте 10-12 метров над земной поверхностью (метры в секунду);
X3 - относительная влажность (%) на высоте 2 метра над поверхностью земли;
R0 - свободный член;
R1, R2, R3 - коэффициенты регрессии.
Исходные данные метеорологических наблюдений были взяты с сайта https://rp5.ru/Архив и записываются в таблицу для удобства вычислений.
Таблица 1.
Исходные данные
|
Год |
Y (ТТ) |
X1 (оС) |
X2 (м/сек) |
X3 (%) |
|
2019 |
20 |
14,9 |
2,6 |
73 |
|
2020 |
15 |
15,4 |
2,4 |
75 |
|
2021 |
45 |
17,5 |
2,4 |
70 |
|
2022 |
21 |
15,6 |
2,2 |
71 |
|
2023 |
25 |
16,5 |
2,1 |
68 |
Для того чтобы рассчитать коэффициенты регрессии воспользуемся формулой:
R=τ*x(σy / σx)
где: R - коэффициент регрессии;
τ – коэффицент корреляции между признаками X и Y;
σy и σx – среднеквадратическое отклонение признаков X и Y, которое определяется по формуле:
![]() где
где ![]()
После всех расчётов получаем данные, которые записываются в таблицу:
|
Год |
Ср. ар. ( |
(X1- |
(X2- |
(X3- |
D |
Квадратный корень |
|
2019 |
30,17 |
233,07 |
759,92 |
1834,69 |
942,56 |
30,70 |
|
2020 |
30,93 |
241,28 |
814,15 |
1941,87 |
999,10 |
31,6 |
|
2021 |
29,97 |
155,42 |
759,92 |
1602,67 |
839,34 |
28,97 |
|
2022 |
29,60 |
196,00 |
750,76 |
1713,96 |
886,91 |
29,78 |
|
2023 |
28,87 |
152,93 |
716,45 |
1531,42 |
800,27 |
28,28 |
Для того чтобы определить коэффициент корреляции воспользуемся пакетными данными MS Excel и получим следующую матрицу парных сравнений:
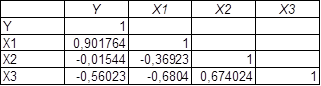
Здесь мы видим, что Y зависит в большей степени от X1, т.е. от температуры воздуха и τ=0,9.
После всех необходимых расчетов мы можем рассчитать коэффициенты регрессии:
R=τ*x(σy / σx).
Рассчитанный коэффициент регрессии, показывает нам, что при изменении признака X на одну единицу, зависимая переменная Y будет изменяться в среднем на 9 единиц.
Рассчитаем среднюю ошибку аппроксимации полученных данных из пакета данных MS Excel по формуле:
ABS=О/Пзн *100%
где: ABS – абсолютные значения
О – остаток
Пзн Y – предсказанное значение Y.
Таким образом, видим, что средняя ошибка аппроксимации составляет 18,6 %, это говорит нам о том, что в среднем прогнозные значения, полученные с помощью этой модели, отклоняются от фактических значений на 18,6%.
Для того, чтобы оценить качество модели линейной регрессии определим коэффициент детерминации, возведя коэффициент регрессии в квадрат. Этот показатель определяет степень линейной связи между переменными. Чем выше значение коэффициента детерминации, тем более точно линейная регрессия соответствует наблюдаемым данным. В этом мы можем убедиться, посмотрев на рис. 1 (график красного цвета).
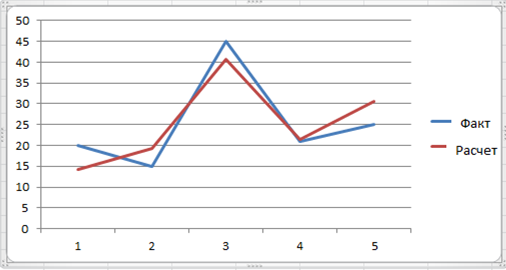
Рисунок 1. Графики фактических и расчетных значений
Делая вывод о регрессионной модели, можно с уверенностью сказать, что данная модель может быть полезным инструментом для системы раннего обнаружения лесных пожаров, позволяя на основе статистических данных о пожарах и погодных условиях определить вероятность возникновения новых пожаров и своевременно предпринять меры для их предотвращения. Для рассматриваемого примера точность модели составила порядка 87 %. В нашем случае была выявлена зависимость метеорологических явлений на количество термоточек, что свидетельствует об адекватности модели.





