Математика в ракурсе экологии

В данной статье рассказывается о тесной взаимосвязи экологии с математикой. Также рассматриваются различные математические методы, применяемые в различных областях экологии.

Не зря математику называют царицей наук, ведь она применятся во многих дисциплинах, даже там, где, казалось, сложно представить ее применение. Поэтому математика и экология тесно связаны. Математика в экологии изучает модели экологических объектов и процессов, а также методы их исследования. Математическая модель учитывает, прежде всего, те ограничения и принципы отбора, которые выделяют реально возможные изменения из числа допустимых.

Экологические процессы моделирует математическая экология. То есть с помощью математике можно предсказать какие изменения произойдут в природе после изменения экологической обстановке.

Одна из главных задач математики в экологии – проблема устойчивости экосистем. Экосистема считается устойчивой и стабильной только тогда, когда численность особей различных видов по отношению друг к другу остается неизменной длительное время[2]. Также рассматриваются оптимизационные задачи управления экосистемами. В качестве измерительного комплекса для этих параметров выступают службы мониторинга. Выделим и рассмотрим основные математические методы, используемые в экологии.

Первый метод – это метод корреляции. В экологических исследованиях часто необходимо получить ответ на вопрос, каковы сила и характер связи между исследуемыми признаками. Для этой цели в математической статистике существует коэффициент корреляции, который оценивает силу связи между количественными признаками. Так, в соответствии с законом экологической корреляции в экосистеме, как и в любом другом целостном образовании, все входящие в нее компоненты функционально соответствуют друг другу. Выпадение одной части системы неминуемо ведет к исключению всех тесно связанных с нею других частей системы и функциональному изменению целого в рамках закона внутреннего динамического равновесия.

Второй метод, распределение Стьюдента – это однопараметрическое семейство абсолютно непрерывных распределений. Распределение Стьюдента имеет важное значение для статистического анализа. С помощью данного распределения можно оценить истинность определенного эксперимента. Для этого необходимо рассмотреть возможные причины ошибок, способствующих повлиять на измеряемую величину.

Следующий метод – это матрица Леопольда. При помощи математического моделирования можно вывести нужные свойства при изменении характеристик модели. Так при помощи матрицы Леопольда можно понять, на сколько пагубно человек влияет на окружающую среду. Данная матрица представляет собой таблицу воздействий, включающую в себя по вертикали список возможных действий (выброс в атмосферу загрязняющих веществ, строительство промышленных зданий и сооружений и т.д.), а по горизонтали – множество потенциальных индикаторов воздействия.

В первых матрицах по горизонтали были перечислены 100 действий, влияющих на окружающую среду, а по вертикали – 88 характеристик окружающей среды. Воздействие, соответствующее пересечению каждого действия и каждого фактора, описывается через его амплитуду и важность. Данные характеристики собственно и служат для определения загрязнения окружающей среды.

Мерой значимости отдельного действия человека в каждом конкретном случае называется важностью. Мерой общего уровня называется амплитудой. Например, вредные выбросы в атмосферу изменяют или вредно влияют на окружающею среду и, таким образом, выбросы могут повлиять на различные группы животного мира и привести к различным мутациям или вообще к исчезновению некоторых популяций. Одна из главных проблем, возникающая при использовании матриц, выражается в том, что они очень громоздки для вычисления, так как матрица имеет 8800 ячеек.

Данные матрицы продолжительное время использовались для оценки воздействия на окружающую среду в США. На данный момент появились более усовершенствованные модели этого метода, в которых намного меньше недостатков, однако общая структура не поменялась.

Для создания моделей экосистем используют методы общесистемного анализа[2]. Сначала выделяют из системы отдельные структурные характеристики, живые и косные компоненты, примером живых – трофические уровни, виды, возрастные или половые группы, взаимодействие данных компонентов определяет поведение всей системы. Затем происходит установление характера процессов, где участвует каждый элемент.

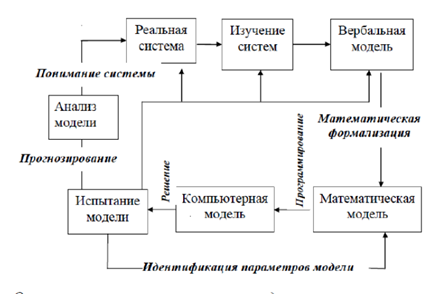
Рисунок 1. Основные этапы математического моделирования

Толчком для развития системных исследований послужила необходимость описывать экологические взаимодействия. Принцип изоморфизма широко применяется для описания систем, позволяющий сходными математическими уравнениями взаимодействовать друг с другом[3].

Работа с имитационной моделью требует знания величин параметров модели, которые могут быть оценены только из наблюдения и эксперимента. Часто приходится разрабатывать новые методики наблюдений и экспериментов с целью установления факторов и взаимосвязей, знание которых позволяет выявить слабые места гипотез и допущений, положенных в основу модели. Процесс моделирования – обладает тщательно отработанной стратегией исследования и строгой проверкой применяемых данных в анализе.

Данное положение, особенно важно для экологии, так как это одна из самых сложных наук, имеющей дело с разнообразными взаимодействиями между огромным множеством организмов и средой их обитания. Поэтому исследование и регулирование экологических процессов представляет собой исключительно сложную задачу.

Изучая литературу в ходе подготовки к написанию этой работы было установлено, что математика решает не только посредственные задачи, но и успешно решает экологические задачи, применяя методы и законы такие как: динамическое моделирование с использованием дифференциальных уравнений, распределение Стьюдента, метод корреляции, матрица Леопольда. Все математические методы сильно облегчают исследование в различных сферах экологии, что позволяет охватить как можно большую часть исследования окружающего мира.

Так зная принципы математического моделирования, человечество может за ранее просчитать последствия принимаемых решений, ведь некоторые из них могут нанести непоправимый вред экологии.