Использование Венгерского метода для решения задачи о назначениях

Введение

Оптимизация процессов является неотъемлемым этапом формирования любого предприятия. Использование Венгерского метода позволяет существенно упростить рационализацию затрат с целью получения максимальной прибыли предприятия.

Основные задачи исследования:

1. Обзор литературы

2. Реализация алгоритма задачи о назначениях

3. Варианты практического применения данного алгоритма.

В первую очередь рассмотрим понятие Венгерского метода. Данный метод является алгоритмом для оптимизации, который используется для решения задачи о назначениях за полиномиальное время. Был создан известным американским математиком Гарольдом Куном в 1955 году. Название “Венгерский алгоритм” получил по причине того, что данный алгоритм брал за основу работы венгерских математиков: Денеш Кёниг и Эгервари Эйген.

Описание алгоритма в виде матричной интерпретации

Для рассмотрения алгоритма поставим задачу: проведение массового мероприятия. Для этого нам необходимы настройка звука, света, оборудования, помещения и заготовка еды для перерывов. Также мы имеем 5 исполнителей, для которых известны оценки эффективности работы по каждой задаче. Нам необходимо максимально эффективное выполнение задач.

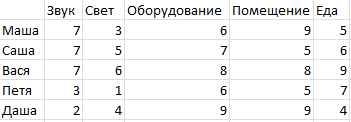
Рисунок 1. Исходные данные

Первым этапом будет нахождение максимальной оценки во всех строках таблицы. Затем нужно значение оценки минусовать из всех элементов строки. После умножаем всю таблицу на (-1).

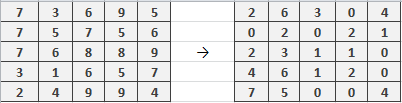
Рисунок 2. Иллюстрация вычисления первого этапа

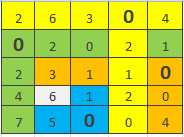
Рисунок 3. Результат вычислений первого этапа

Затем нужно выбрать нули так, чтобы во всех строчках и столбцах он был единственный. В нашей матрице это сделать нельзя. Поэтому дальше меняем таблицу, но уже находим в строке/столбце наименьшее значение и минусуем его из значений строки/столбца.

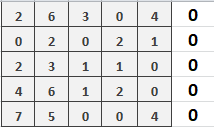
Рисунок 4. Нахождение нулей в каждой строке

Рисунок 5. Нахождение минимального элемента в строке/столбце и вычитание его из элементов строки/столбца

Затем нужно определить нули так же, как мы делали на первом этапе:

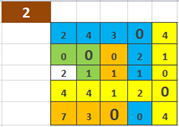
Рисунок 6. Нахождение нулей

Следующим шагом вычеркиваем столбцы, содержащие нули так, чтобы количество перечёркивающих линий было наименьшим. Из остальных значений выбираем меньший, минусуем его из других элементов и складываем с значениями, которые находятся на пересечениях вычеркиваний.

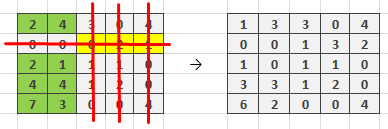
Рисунок 7. Последний этап

В итоге получаем матрицу, показывающую самое эффективное распределение задач по исполнителям.

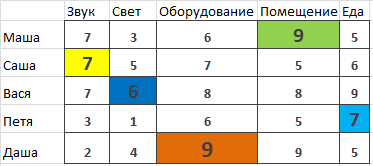
Рисунок 8. Итоговая матрица

Практическое применение

• Задача о распределении должностей между работниками компании. Достижение максимальной эффективности и минимальных затрат при распределении должностей
• Отбор кандидатов на различные должности по определенным критериям эффективности.
• Рационализация автомобильного производства. Распределение производственного конвейера для снижения затрат на содержание.
• И многие другие.