Применение деревьев в кодировании информации

В современном стремительно развивающемся мире высоких технологий особую значимость приобретают  математические разделы, имеющие отношение к развитию ЭВМ. Одним из таких разделов является теория графов. Это связано с тем, что с помощью графов можно легко описать огромное количество различных объектов и ситуаций с ними. Именно поэтому исследование теории графов не утрачивает своей актуальности в разработке различных оптимизационных алгоритмов.

Цель работы: закодировать информацию с использованием методов теории графов и теории информации.

Задачи:

1. Рассмотреть основные определения и характеристики деревьев.

2. Изучить и сравнить два наиболее популярных алгоритма кодирования и декодирования информации (Шеннона - Фано и Хаффмана).

3. Построить дерево кодирования.

4. Выбрать наиболее эффективный метод кодирования.

Определения из теории графов

Граф — это объект, состоящий из конечного множества вершин и множества ребер, где каждое ребро есть подмножество множества вершин мощности 2.

Граф называется связным, если любые две его вершины связаны.

Дерево - это связный граф, не содержащий циклов.

Упорядоченное дерево – это дерево, в котором множество потомков каждой вершины упорядочено.

Бинарное дерево – это упорядоченное дерево, в котором каждая вершины имеет не более 2 потомков.

Связь теории графов и теории информации

Теория графов является инструментом различных областей науки. Не маловажную роль бинарные деревья играют и в теории информации - это такой раздел прикладной математики, и информатики, относящийся к измерению количества информации, её свойств и устанавливающий предельные соотношения для систем передачи данных.

Кодирование применяется для того, чтобы минимизировать число бит в единицу времени, необходимых для представления выходных данных источника. Этот процесс известен как кодирование источника или сжатие данных.

Алгоритм Шеннона – Фано

Код строится следующим образом. Кодируемые знаки выписывают в таблицу в порядке убывания их вероятностей в сообщениях. Затем их разделяют на две группы так, чтобы значения сумм вероятностей в каждой группе были близкими. Все знаки одной из групп в соответствующем разряде кодируются, например, единицей, тогда знаки второй группы кодируются нулем. Каждую полученную в процессе деления группу подвергают вышеописанной операции до тех пор, пока в результате очередного деления в каждой группе не останется по одному знаку.

Алгоритм Хаффмана

Кодируемые знаки располагают в порядке убывания их вероятностей. Далее на каждом этапе две последние позиции списка заменяются одной и ей приписывают вероятность, равную сумме вероятностей заменяемых позиций. После этого производится пересортировка списка по убыванию вероятностей. Процесс продолжается до тех пор, пока не останется единственная позиция с вероятностью, равной 1.

Теперь рассмотрим алгоритмы Шеннона - Фано и Хаффмана на примере задач.

Задача №1. Закодировать по методу Шеннона - Фано сообщение: Информационная безопасность автоматизированных систем

Решение:

1. Количество символов исходного сообщения равно 53.

2. Занесем в таблицу 1 частоты появления символов (вероятности) и проранжируем их.

 Таблица 1.

Таблица частот появления символов

1. Поделим символы на 2 группы с примерно равной частотой появления. Символам первой группы присваиваем “0”, второй группы - “1”. Полученные группы делим на подгруппы и продолжаем процесс. Строим кодовое дерево (см. рисунок 1).

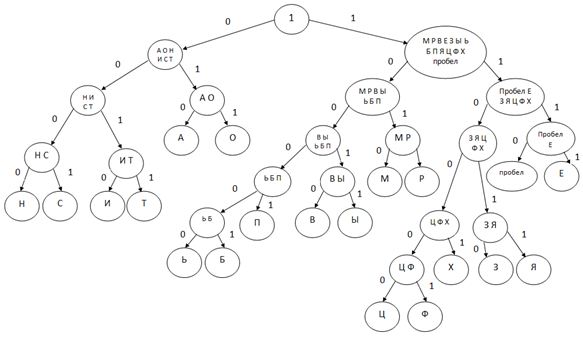
Рисунок 1. Кодовое дерево

Составим таблицу соответствия символов с полученным кодом Шеннона -Фано.

Таблица 2.

Таблица соответствия символов с полученным кодом Шеннона - Фано

Ответ: полученное закодированное сообщение имеет вид: 001000001100010111011101001011000000100110000000001011011111101000011111110100111000101000010000011000100111000001110010100100011011101001000110010110100010101101110010010000010011110011110000100100001001111111010. Объём: 213 бит.

Задача №2. Закодировать по методу Хаффмана сообщение: Информационная безопасность автоматизированных систем

Решение:

1. Проранжируем символы в порядке убывания.

2. Объединим два последних символа в один, заменив на их сумму. Продолжаем процесс, до появления единственной позиции с вероятностью 1.

Таблица 3.

Алгоритм Хаффмана

3. Построим кодовое дерево. Корню нашего кодового дерева присваиваем 1. Далее каждой вершине присваиваем по 2 потомка со значениями вероятностей, которые участвовали в образовании этой вершины. Продолжаем процесс (см. рисунок 2).

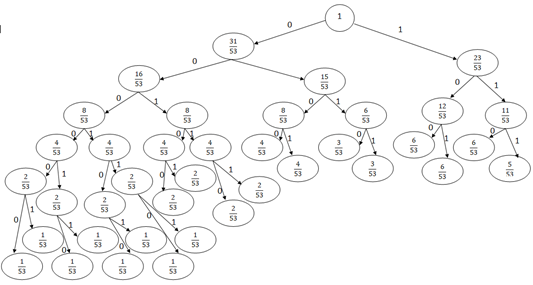
Рисунок 2. Кодовое дерево

Заносим в таблицу 4 соответствия символов с полученным кодом Хаффмана.

Таблица 4.

Таблица соответствия символов с полученным кодом Хаффмана

Ответ: 111101000000110010000111100000001111110101101100000010011000001101001010101100001001000010101110001000110001010110100010110011110011110000111110101011101000110010111001011010001100001110110001011100100011010010111.

Удостоверимся в эффективности сжатия Хаффмана. Для этого подсчитаем объёмы исходного сообщения в кодировке ASCII и закодированного по методу Хаффмана и сравним их.

Для расчета объёма сообщения после кодирования алгоритмом Хаффмана воспользуемся таблицами 1 и 4 и просуммируем произведение частоты появления символов и количества 0 и 1, которые соответствуют этому символу.

I₁=6*3+6*3+6*3+5*3+4*4+4*4+3*4+3*4+2*5+2*5+2*5+2*5+6*8=213 бит.

Один символ в памяти компьютера занимает 1 байт или 8 бит.

Объём сообщения I₂ в кодировке ASCII, находится по формуле:

I₂ = n*i,

где: n — количество всех символов сообщения,

i — вес 1 символа в битах,

В нашей задаче n = 53, i = 8 бит, значит, I₂ = 8*53 = 424 бит.

Коэффициент сжатия: 

Вывод

В закодированном нами сообщении получилось одинаково 213 символов при использовании двух разных методов. Достаточно сложно подобрать пример показывающий разное количество символов.

На наш взгляд, методика Шеннона – Фано является достаточно старым методом сжатия, на сегодняшний день оно не представляет особого практического интереса и не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы на 1-й итерации можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу. В результате среднее число символов на букву окажется другим. Таким образом, построенный код может оказаться не самым лучшим.

От указанного недостатка свободна методика Хаффмана. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву. И именно поэтому метод Хаффмана много эффективней.

В нашей работе мы рассмотрели основные понятия теории графов и теории информации, описали два алгоритма кодирования и построили кодовое дерево. С помощью кодового дерева очень удобно кодировать и тем самым сжимать сообщения, а методы теории графов позволяют решать такие задачи проще и интереснее.