Негамильтоновы графы

Введение

Многие открытия теории графов были использованы для решения «практических» проблем – задач, головоломок, игр и т.д. В 1859 г. известный математик – сэр Уильям Гамильтон – придумал игру, в которой требуется обойти замкнутый контур всех ребер додекаэдра, минуя каждую вершину лишь один раз. В теории графов эта игра эквивалентна определению остовного цикла, содержащего все 20 вершин. Все графы, в которых существует подобный цикл, называются гамильтоновыми. Если в графе «много» рёбер, (например, степень каждой вершины больше или равна половине числа вершин, то в таком графе существует гамильтонов цикл. В остальных нетривиальных случаях вопрос о существовании гамильтонова цикла остаётся открытым.

Постановка проблемы

Необходимая и достаточная теорема о существовании гамильтонова цикла, которая была бы применима ко всем графам, до сих пор не найдена. Есть теоремы, описывающие условия, при которых существует гамильтонов цикл, но они не охватывают все графы. Поэтому цель нашей работы – сформулировать и доказать достаточный признак отсутствия гамильтонова цикла в графе.

Основные определения

Введем некоторые определения, которые будут использованы в работе.

Определение 1. Маршрут – чередующаяся последовательность вершин и ребер, начинающаяся и заканчивающаяся вершиной, в которой любые два соседних элемента инцидентны. Путь – маршрут, все ребра которого различны. Одна вершина также является путем.

Определение 2. Цикл – путь в графе, в котором начальная и конечная вершины совпадают.

Определение 3. Компонента графа – некоторое подмножество вершин графа, такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества. Одна вершина также является компонентой.

Определение 4. Гамильтонов цикл – цикл в графе, содержащий все вершины графа ровно по одному разу [1].

Вспомогательные теоремы

Лемма 1. Предположим, что k вершин были удалены из цикла С. Тогда останется p несоединенных путей, таких что p ≤ k.

Доказательство. Докажем лемму 1 с помощью метода математической индукции.

1)  База индукции. Допустим k = 1 для цикла из произвольного числа вершин, как на рисунке 1. Тогда если k = 1, то останется только 1 путь, доказывая справедливость леммы для k = 1.

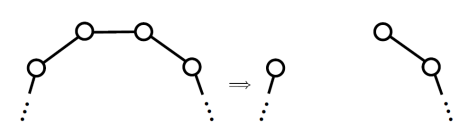
Рисунок 1. Удаление одной вершины из цикла

2)  Предположение индукции. Теперь предположим, что лемма 1 справедлива для k вершин. Удаляем k вершин из цикла С, порождая p несоединенных путей и .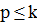

3)  Шаг индукции. Допуская, что лемма 1 справедлива для k вершин, докажем, что ее справедливость сохраняется и для k + 1 вершин.

После удаления вершины из цикла C, число новых несоединенных путей p' может получится равным:

                                             (1)

Пусть число удалённых вершин:

k' = k + 1                                                                                    (2)

Согласно предположению индукции, утверждение p ≤ k верно. Тогда следующие неравенства также будут справедливы:

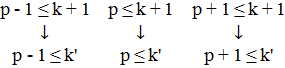                                                         (3)

Используя (1) и (2) доказано, что p' ≤ k'.

Таким образом, допуская, что лемма 1 справедлива для k вершин, ее справедливость сохраняется и для k + 1 вершин. Лемма 1 доказана.

Теорема 1. Пусть дан гамильтонов граф G, тогда удаление n вершин породит m несоединенных компонент, таких, что m ≤ n.

Доказательство. Данный граф G - гамильтонов, значит, в нем есть гамильтонов цикл, который обозначим как H. По лемме 1, когда мы удалим n вершин из H, останется m_H несоединенных путей, причём m_H ≤ n. Так как пути не соединены, они являются компонентами. Если граф G содержит только ребра из цикла H и никаких других, то число компонент останется m и m = m_H, тогда теорема доказана, так как m_H ≤ n из чего следует m ≤ n. Однако, если в графе G есть ребра, не входящие в гамильтонов цикл H, эти ребра могут соединять некоторые m_H компоненты при удалении n вершин. Обозначим фактическое число компонент как m и m < m_H, так как возможное объединение компонентов уменьшает фактическое их число. Так как m ≤ m_H и m_H ≤ n, то m ≤ n. Таким образом, при удалении n вершин из графа G, число компонент будет m и m ≤ n. Теорема доказана.

Основная теорема

Теорема 2. Пусть G - такой граф, что удаление n вершин породит m несоединенных компонент, таких что m > n, тогда G - негамильтонов.

Доказательство. Предположим противное, пусть исходный граф G – гамильтонов. Если G – гамильтонов, тогда удаление n вершин из G породит m несоединенных компонент таких что m ≤ n согласно теореме 1. Это противоречит условию m > n. Таким образом, предположение оказалось неверно и граф G не может быть гамильтоновым. Теорема доказана.

Пример. Продемонстрируем работу теоремы на конкретном примере. Пусть дан граф, изображенный на рисунке 2(a).

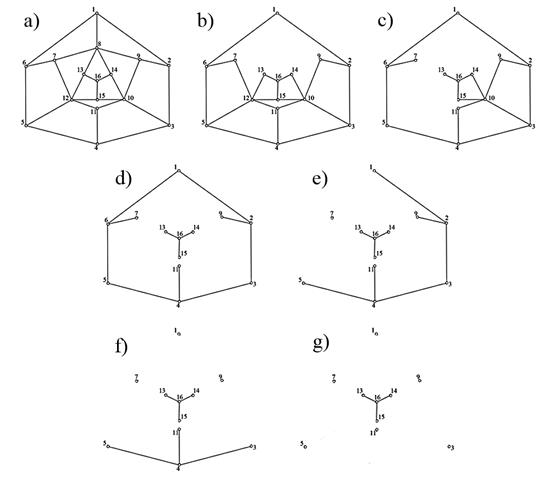
Рисунок 2. Иллюстрация к примеру

Удалим вершину 8. При удалении вершины удаляются и все инцидентные ребра. Получаем граф, изображенный на рисунке 2(b). При удалении несоединенных компонент не появилось. Далее удалим вершину 12. Граф будет иметь вид как на рисунке 2(c). Число удаленных вершин n=2, новые компоненты связности не образовались. Удалим вершину 10, получаем ситуацию, изображенную на рисунке 2(d). Образовалось две компоненты связности: {13, 14, 15, 16} и {1, 2, 3, 4, 5, 6, 7, 9, 11}. Получаем n=3, m=2. Удалим вершину 6, рисунок 2(e). Теперь стало три компоненты связности: {13, 14, 15, 16}, {7} и {1, 2, 3, 4, 5, 9, 11}. Количество удаленных вершин n=4, число компонент связности m=3. Пока условие теоремы не выполняется, продолжаем удаление вершин. Удалим вершину 2, рисунок 2(f). Тогда n=5, m=5. Из рисунка видно, что вершины 4 и 16 инцидентны трем ребрам, то есть для появления новых компонент связности целесообразнее было бы удалить одну из них. Удалим вершину 4, получим граф, изображенный на рисунке 2(g). Заметим, что теперь образовалось 7 компонент связности, а количество удаленных вершин равно 6. Таким образом, m = 7, n = 6, 7 > 6. Получаем, что m > n удовлетворяет условию теоремы, доказывая, что граф на рисунке 2(a) не содержит гамильтонова цикла.

Заключение

В данной работе нами были сформулированы и доказаны теоремы, отражающие связь между гамильтоновыми графами и компонентами связности (Лемма 1 и Теорема 1). На их основании была сформулирована и доказана достаточная теорема о несуществовании гамильтонова цикла в графе (Теорема 2). Стоит отметить, что данная теорема не является необходимой для отсутствия гамильтонова цикла. Все графы, показывающие, что условие не является необходимым, могут быть отнесены к негамильтоновым другими методами.