Теорема существования решения бесконечной системы обыкновенных дифференциальных уравнений

Первой по времени теоремой существования и единственности решения бесконечной системы нелинейных дифференциальных уравнений

была теорема, принадлежащая А. Н. Тихонову [6].

Относительно правых частей системы (1) предполагается, что:

1) функции  определены при  в области D:

2) функции  непрерывны по совокупности переменных  при фиксированном 

3) при фиксированных  функции  измеримы по 

4) при произвольном выборе переменных  из области D функции  удовлетворяют условиям

для всех  где  функция положительная, суммируемая в отрезке: 

5) интеграл Лебега от функции  ограничен

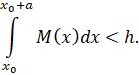
Итак, рассмотрим бесконечную систему (1).

Теорема. (А. Н. Тихонов). Если выполняются условия 1)–5), то существует, по крайней мере, одна система решений системы уравнений (1), удовлетворяющая начальным условиям

где  произвольная система начальных значений.    

Доказательство: Заметим, что если в функции  вместо  подставить измеримые функции  определенные в промежутке  то в результате получим измеримые и ограниченные функции

которые, следовательно, являются интегрируемыми по 

Заменим систему дифференциальных уравнений (1) системой интегральных уравнений

и рассмотрим соответствующее ей функциональное преобразование

ставящее в соответствие всякой счетной системе непрерывных функций  другую систему функций 

Если существует система, инвариантная при этом преобразовании, то она представляет собой решение интегральных уравнений (4), а следовательно, и системы дифференциальных уравнений (1), удовлетворяющее начальным условиям (3).

Рассмотрим пространство , за точку которого возьмем счетную совокупность непрерывных функций , равноограниченных некоторым числом K, называемых компонентами или координатами этой точки. Пусть точки P и Q этого пространства имеют соответственно координаты Запишем это так:

Введем теперь в пространстве  метрику, т.е. определим расстояние между двумя точками этого пространства следующим образом:

Пространство  будет полным метрическим пространством. Норму элементов  пространства определим следующим образом:

Пространство  будет полным линейным нормированным пространством.

Возьмем в пространстве  множество В, состоящее из точек

  координаты которых удовлетворяют условиям:

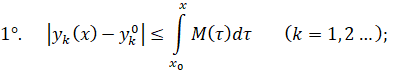
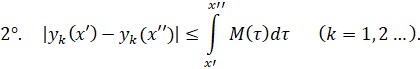
Покажем, что множество В является замкнутым, выпуклым и компактным. Действительно, пусть  счетная последовательность точек из В, координаты которых функции  согласно  и  , равномерно ограничены и равностепенно непрерывны. Тогда по теореме Арцела из последовательности  можно выбрать подпоследовательность  равномерно сходящуюся к некоторой функции 

Аналогично из последовательности  можно выбрать подпоследовательность , равномерно сходящуюся к  и т.д. Таким образом, последовательность точек  сходится к точке  так как

равномерно для всякого m.

Итак, для любого  совокупность координат  оказалась компактной.

Если точки  принадлежат множеству В, то и точка  принадлежит множеству В, так как условия  и   допускают предельный переход.

Так что условие замкнутости множества В выполняется.

Если две точки множества В, то точка

принадлежит тому же множеству, так как она соответствует системе функций

определяющей точку множества В. Отсюда следует, что множество В выпуклое.

Докажем теперь, что преобразование (5) непрерывно.

Пусть  предел последовательности точек

оператор, определяемый уравнениями (5).  Тогда получим:

Согласно условиям теоремы, для  существуют такие  что из условий

следует

Выбирая i достаточно большим в силу (7), получаем 

что доказывает непрерывность преобразования (5). 

Покажем теперь, что система функций определяемая равенствами (5), принадлежит вновь множеству В.

Действительно, условия  и   выполняются и для этих функций:

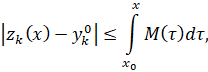
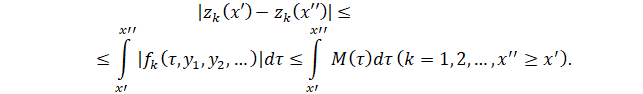
Таким образом, в полном линейном нормированном пространстве  непрерывный оператор  отображает замкнутое, выпуклое и компактное множество В в его часть. Пользуясь теоремой Шаудера, можно заключить, что при этом отображении существует хотя бы одна неподвижная (инвариантная) точка  Система функций  соответствующая этой точке  и будет являться решением системы интегральных уравнений (4) или задачи (1)(3).