Анализ понятий импульс и обобщенный импульс в уравнениях динамики

Аннотация. Осуществляется анализ понятий импульс и обобщенный импульс в механике Ньютона, Лагранжа, Гамильтона. Рассмотрена связь обобщенного импульса и векторного потенциала. Производится сравнительный анализ использования обоих понятий в уравнениях движения нерелятивистской заряженной частицы в переменном магнитном поле. Обосновано преимущество уравнений Гамильтона.

Abstract. The concepts of momentum and generalized momentum in the mechanics of Newton, Lagrange, and Hamilton are analyzed. The relationship between the generalized momentum and the vector potential is considered. A comparative analysis of the use of both concepts in the equations of motion of a non-relativistic charged particle in an alternating magnetic field is performed. The advantage of Hamilton's equations is proved.

Ключевые слова: импульс; обобщенный импульс; механика Ньютона, Лагранжа, Гамильтона; динамическое уравнение.

Keywords: momentum; generalized momentum; Newton, Lagrange, Hamilton mechanics; dynamic equation.

В классической механике понятию импульс могут соответствовать отличные, но математически связанные друг с другом понятия. Ньютон [1] определяет импульс  как меру количества движения, устанавливаемую пропорционально скорости  и массе  материальной точки .

В трактате «Аналитическая механика» [2] Лагранж вводит понятие обобщенного импульса  и определяет его как частную производную скалярной функции – функции  Лагранжа  по скорости.

В настоящее время оба понятия имеют широкое применение при задании механического движения в форме обыкновенных дифференциальных уравнений.

Целью данной работы является сравнительный анализ использования обоих понятий при описании движения нерелятивистской заряженной частицы в переменном магнитном поле.

1. Уравнения Ньютона и Лагранжа

Рассмотрим движение нерелятивистской частицы с массой  в декартовой системе координат в инерциальной системе отсчета. Динамическое уравнение Ньютона частицы может быть записано в двух формах:

,                                     (1)

где  – скорость частицы;  – её импульс;  – сила, действующая на частицу как функция её положения, скорости и, вообще говоря, времени .

Если , то имеет место интеграл движения , называемый законом сохранения импульса.

Стоящие в левых частях уравнений (1) выражения можно представить как градиенты скалярных функций ,  по векторному аргументу скорости   и импульса , соответственно, поскольку

.                                 (2)

Функции  – выражают кинетическую энергию материальной точки.  

Используя (2), динамические уравнения (1) можно записать в формах:

 .                             (3)

Предположим, что стоящая в правых частях сила зависит только от координат . Пусть, кроме того, сила может быть представлена в виде градиента некоторой силовой функции  по аргументу радиус-вектора. Иными словами, сила выражается потенциальным полем [3]. Тогда уравнения (3) могут быть записаны в формах:

,                                             (4)

,                                             (5)

где функция , определяет потенциальную энергию частицы [3].

Таким образом, если действующая на материальную точку сила потенциальна, то динамические уравнения (1), связывающие векторные функции , могут быть преобразованы к динамическим уравнениям, связывающим скалярные функции .

Динамическое уравнение (4) – есть уравнение Лагранжа движения материальной точки в декартовой системе координат в инерциальной системе отсчета [3].

Пользуясь тем, что потенциальная энергия не зависит от скорости материальной точки, а её кинетическая энергия не зависит от декартовых координат,  уравнение Лагранжа можно записать в виде:

,                                                     (6)

где  – функция Лагранжа.

В частности, уравнение Лагранжа (6) свободной материальной точки

.                                       (7)

Из выражений (6), (7) следует, что функция Лагранжа связана с классическим импульсом соотношением . С другой стороны, градиент функции Лагранжа по векторному аргументу скорости определяет обобщенный импульс материальной точки . Таким образом, обобщенный импульс частицы в потенциальном поле в декартовой системе координат совпадает с импульсом Ньютона .

2. Векторный потенциал

При выводе уравнения Лагранжа из уравнения Ньютона мы ограничились силами, зависящими только от декартовой координаты материальной точки и, кроме того, представимой в форме градиента силовой функции. Это позволило нам перейти к динамическому уравнению Лагранжа, связывающему скалярные функции. Естественно возникает вопрос: нельзя ли аналогичным образом поступить с силой, зависящей и от скорости.   

Конкретизируем задачу. Во-первых, можно ли определить такую силу , которая, кроме того, зависит от скорости  и допускает представление в форме интеграла движения. Во-вторых, если такая абстракция возможна, будет ли она иметь практический смысл.

Пусть  – такая сила. Закон Ньютона запишется для нее в форме:

.                                            (8)

Чтобы получить интеграл движения, необходимо представить функцию  в форме полного дифференциала от скалярной функции, зависящей от скорости. Замечаем, что в вышеприведенных рассуждениях мы именно так представили вектора скорости. Действительно, у нас было: , то есть кинетическая энергия являлась «потенциалом» для функций скоростей. Запишем закон Ньютона в виде:

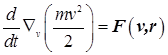 .                                           (9)

Из выражения (9) следует необходимость выполнения условия:

 ,                                           (10)

где  – некоторое скалярное поле по векторным аргументам радиус-вектора и скорости. Тогда закон Ньютона (8) вновь можно привести к уравнению Лагранжа (6). Сила, удовлетворяющая условию (10), называется обобщенно-потенциальной силой [3].

Проанализируем возможный вид функции . Уравнение (10) означает, что, если функция  тождественно не равна нулю, то она зависит от скорости, но лишь линейно. В противном случае, после взятия внешней производной по времени у нас получилась бы сила , зависящая от ускорений и нарушающая принцип детерминированности Ньютона [4]. Поскольку  – вектор, а  – скаляр, то единственно возможная  зависимость, с точностью до знака, определяется выражением:

,                                                     (12)

где  – векторное поле, называемое векторным потенциалом [3];  – произвольная постоянная величина.

Если сила  имеет вид (10), то уравнение (9) приводится к виду:

.                  (13)

Сравнивая (13) с уравнением Лагранжа свободной материальной точки (7), видим, что уравнения будут иметь одинаковую форму, если положить

.                                        (14)

Таким образом, динамическое уравнение Лагранжа движения материальной точки в поле векторного потенциала (12) формально совпадает с уравнением Лагранжа (6) свободной частицы.

По определению Лагранжа, градиент функции Лагранжа по векторному аргументу скорости есть обобщенный импульс:

.                                       (15)

Следовательно, импульс и обобщенный импульс в случае движения материальной точки в поле векторного потенциала связаны уравнением:

.                                                    (16)

Если векторный потенциал зависит от времени явно, то из (16) следует

.                                                    (17)

Подставляя функцию Лагранжа (14) в уравнение (6), мы видим, что обобщенный импульс частицы в поле векторного потенциала является интегралом движения. Её динамическое уравнение  формально совпадает с уравнением движения свободной частицы . Тем не менее, движения будут существенно различны. В частности, если для классического импульса выполнено условие , то мы немедленно получаем прямолинейное равномерное движение материальной точки со скоростью . В случае же обобщенного импульса сохраняется величина, определяемая выражением (16) и движение будет не прямолинейным и не равномерным.

3. Движение материальной точки в электромагнитном поле

Мы определили условие, при котором зависящая от скорости сила может входить в уравнение Лагранжа в форме скалярного поля. Но при этом не ясно, может ли такая сила являться математической моделью какой-либо физической реальности. Таким образом, решим вторую из поставленных задач.

Формализуем задачу. Легко видеть, что нам необходимо преобразовать уравнение (6) с функцией Лагранжа (14), имеющее вид

,                                                 (18)

к классическому уравнению Ньютона (1) и определить: будет ли стоящая в правой части уравнения сила Ньютона иметь практическую реализацию.

Из (18) следует, что элементарное приращение импульса определяется полным дифференциалом векторного потенциала, т.е. . Полный дифференциал векторного поля можно разложить на три составляющие: . Тангенциальная составляющая  изменяет абсолютную величину импульса. Нормальная составляющая . изменяет направление импульса. Наконец  отражает возможность явной зависимости векторного потенциала от времени.

Поскольку нормальная составляющая  изменяет только направление вектора импульса, то её можно представить в форме векторного произведения элементарного перемещения  на ротор векторного потенциала:

.                                              (19)

Дифференциал же тангенциальной составляющей  может быть выражен через дивергенцию векторного потенциала в виде:

.                                                   (20)

Заметим, что к настоящему времени нет эмпирических фактов существования поля, реализующего эту составляющую. Тем не менее, для общности анализа мы не будем исключать её из динамического уравнения.

Наконец, временная составляющая может быть записана в форме:

.                                            (21)

Она изменяет величину импульса, если векторный потенциал зависит от времени явно.

Подставим (19), (20), (21) в уравнение (18) и перепишем его в виде:

.                                  (22)

Если теперь определить , , , , где  – индукция магнитного поля;  – напряженность индукционного электрического поля;  – электрический заряд материальной точки, то динамическое уравнение (22) будет иметь форму второго закона Ньютона для заряда, движущегося в переменном магнитном поле [3]:

                                                  (23)

Из определения импульса  следует дифференциальное уравнение:

.                                                          (24)

Дифференциальные уравнения (23), (24) реализуют импульсное представление при исследовании движения нерелятивистских заряженных частиц в переменном магнитном поле.

4. Уравнения Гамильтона

Выведем теперь динамические уравнения движения заряженной частицы в переменном магнитном поле, используя концепцию обобщенного импульса.

Умножая обе части уравнения (18) на произведение , получим . Используя уравнения (15) и (16) преобразуем выражение (18) к виду , откуда следует интеграл движения в форме:

.                                     (25)

Функция (25) определяет функцию Гамильтона частицы в магнитном поле [3].

Возьмем полную производную выражения  (25):

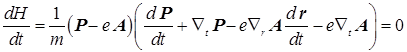.               (26)

Для движущейся заряженной  частицы из уравнения (26) следует уравнение:

,                                    (27)

где . Условие (17) в случае  означает . Поэтому второе и четвёртое слагаемые уравнения (27) дают ноль.

Разрешим уравнение (15) относительно  и, полагая ,  запишем:

,                                                 (28)

или в форме обыкновенного дифференциального уравнения первого порядка:

.                                                 (29)

Используя (28)  приводим выражение (27) также  к форме обыкновенного уравнения первого порядка:

.                                           (30)

Динамические уравнения (29), (30) называются уравнениями Гамильтона  заряженной частицы в поле векторного потенциала. Они позволяют исследовать движение нерелятивистских частиц в переменном магнитном поле на основе использования концепции обобщенного импульса и векторного потенциала электромагнитного поля.

Использование векторного потенциала в уравнениях Гамильтона (29), (30)  позволяет свести движение частицы  к движению в одном векторном поле . В то время как соответствующие уравнения Ньютона (23) требуют использования двух векторных полей и . Кроме того, наличие векторного произведения, как правило, усложняет решение уравнений. Эти факторы делают использование уравнений Гамильтона предпочтительным. 

Заключение

Мы осуществили сравнительный анализ использования понятий импульса и обобщенного импульса в динамике нерелятивистской материальной точки. Получены следующие основные результаты:

1. В декартовой системе координат для материальной точки, движущейся в потенциальном поле, её импульс равен обобщенному импульсу. Условие потенциальности силы позволяет перейти от динамических уравнений в форме Ньютона к динамическим уравнениям в форме Лагранжа.

2. При движении материальной точки под действием обобщенно потенциальной силы введение обобщенного импульса позволяет привести динамическое уравнение Ньютона к форме динамического уравнение Лагранжа и наоборот. При этом импульс частицы и её обобщенный импульс, существенно, разные величины.

3. Движение нерелятивистских частиц в переменном магнитном поле может быть задано на основе использования импульса в форме динамических уравнений Ньютона или на основе использования концепции обобщенного импульса  в форме уравнений Гамильтона.