Разработка программного обеспечения для реализации Венгерского алгоритма для решения задачи о назначениях

Одними из самых актуальных задач линейного программирования на сегодняшнее время являются задачи транспортного типа. Их применение достаточно широко. Наиболее часто они используются в транспортных копаниях, аэропортах, системе трубопроводов, а также на различных производствах.

Проблема программной реализации становится весомой не только из-за сложности алгоритмов, направленных на решение данных задач. Если говорить о таких больших моделях, как аэропорт, то следует помнить о масштабах используемых данных. Достаточно сложно вручную просчитать расписание авиарейсов различных компаний и исключить возможные ошибки. Отсюда исходит необходимость в создании такого ПО, которое сможет не только оказать помощь в решении тех или иных задач, но также будет оперировать достаточно большим объемом данных.

Решение самой транспортной задачи направлено на минимизацию транспортных издержек или максимизацию прибыли при перевозках однотипных грузов от нескольких поставщиков к нескольким потребителям. Причем все поставщики и потребители расположены в различных местах [1].

Задача о назначениях в свою очередь используется для качественного анализа ситуаций, в которых оказывается менеджер при наборе персонала или распределении обязанностей между рабочими. Так же задачу о назначениях можно использовать при назначении операций различным производственным машинам.

Каждый из рабочих или машин могут выполнить тут или иную работу с различной степенью эффективности, которая напрямую влияет на материальную выгоду. При этом так же следует учитывать затраты различных ресурсов на выполнение этой работы. Поэтому распределение или назначение должно происходить с учетом либо наибольшей эффективности (выгоды), либо наименьших затрат (издержек) [2].

С математической точки зрения можно рассматривать задачу о назначениях как частный случай транспортной задачи, поскольку по сути своей они преследуют аналогичные цели.

Рассмотрим более подробно постановку задачи о назначениях.

Постановка задачи. В наиболее общей форме задача формулируется следующим образом:

Имеется некоторое число работ и некоторое число исполнителей. Любой исполнитель может быть назначен на выполнение любой (только одной) работы, но с неодинаковыми затратами. Нужно распределить работы так, чтобы выполнить работы с минимальными затратами. Если число работ и исполнителей совпадает, то задача называется линейной задачей о назначениях. Количество работ и исполнителей может разниться [3].

Математическая постановка задачи. Введем несколько вспомогательных определений.

Пусть имеются  работников,  должностей и мера стоимости работника  на должности  равна . Компоненты  образуют матрицу , будем называть ее матрицей распределения.

Булева матрица |||| размера  такая, что     

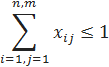
называется матрицей назначения.

Если

то матрица назначения называется насыщенной.

Используя выше обозначенные термины, сформулируем задачу о назначениях.

Дана матрица распределения . Необходимо найти для нее насыщенную матрицу назначения ||||, для которой

Любая задача о назначениях может быть решена с использованием методов линейного программирования или алгоритма решения транспортной задачи. Однако в виду особой структуры задачи, для нее был разработан специальный Венгерский алгоритм.

Идея Венгерского метода заключается в том, чтобы найти значения, которые впоследствии вычитаются из всех элементов каждой строки и столбца. Причем вычитаемые значения должны быть такими, чтобы все элементы матрицы после процедуры вычитания остались неотрицательными. Таким образом, значение приведенной целевой функции становится нулевым, а значит, оптимальным.

Для реализации алгоритма был выбран современный высокоуровневый язык программирования общего назначения Python, который является мощным инструментом для создания различного рода программ.

Пример. Рассмотрим результат применения, разработанного ПО к некоторой задаче. Все этапы решения для наглядности проиллюстрированы (Рис 1).

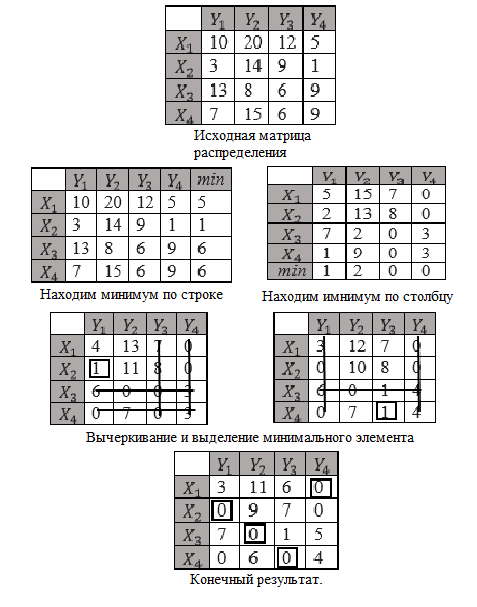
Рисунок. 1. Этапы решения задачи

Исходя из рисунка 1 решение целевой функции:

На рисунке 2 изображены результаты работы ПО.

Рисунок. 2. Результат работы ПО

Как видно из рисунка 2, результаты вычислений и результаты работы ПО совпадают. Из этого можно сделать вывод, что язык программирования Python позволил создать эффективное ПО, с помощью которого можно решать различные прикладные задачи.

Список литературы:

1.  Агальцов, В.П. Математические методы в программировании: учебник. В.П. Агальцов, И.В. Волдайская. - М.: ИД «ФОРУМ»: ИНФРА-М, 2006 г. - 224 с.

2. Волков И.К., Загоруйко Е.А. Исследование операций: Учеб. для вузов. 2-е узд. / Под ред… В.С. Зарубина, А.П. Крищенко. – М.: Узд-во МГТУ им. Н.Э. Баумана, 2002. – 436 с.

3. Кофман А. Введение в прикладную комбинаторику. Под ред. Б.А. Севастьянова – М.: «Наука», 1975 г. – 474 с.

4.  Эддоус М., Стэнсфилд Р. Методы принятия решений/ Пер. с англ. под ред. член-корр. РАН И.И. Елисеевой. — М.: Аудит, ЮНИТИ, 1997. — 590 с.