Пример обработки и визуализации статистических данных на основе программы Excel

В работе на примере одной задачи рассмотрены различные виды статистических распределений и графического представления данных с помощью редактора электронных таблиц Excel. Показано, как формируется статистический ряд, простой и расширенный вариационные ряды, описана последовательность действий по построению графиков распределения частот, гистограммы, кумуляты, огивы.

В различных сферах практической деятельности специалисты сталкиваются с необходимостью анализировать большой поток информации, полученной в результате каких-либо наблюдений или измерений [5, с, 1270–1271]. Грамотно сформулировать выводы на основании этих данных и оценить надежность полученных результатов позволяют методы математической статистики. Конечно, в эпоху компьютеризации обработка информации должна производиться автоматизировано [2, с. 39–46]. Одной из общедоступных программ, позволяющих осуществлять анализ и визуализацию статистических данных, является Excel стандартного пакета Microsoft Office. В данной работе пошагово рассматривается процесс обработки медицинской информации на примере конкретной статистической задачи.

Условие задачи: На основании анализа историй болезней получены следующие значения сроков лечения заболевания (n = 50 пациентов): 16, 14, 17, 15, 20, 16, 17, 18, 15, 13, 18, 16, 14, 17, 12, 19, 16, 15, 17, 18, 14, 19, 16, 18, 15, 17, 13, 16, 20, 15, 21, 17, 15, 16, 13, 16, 19, 18, 14, 15, 15, 16, 17, 14, 16, 19, 21, 15, 17, 18. Построить полигон распределения частот, гистограмму, кумуляту, огиву [3, с. 108].

Решение задачи разобьем на отдельные шаги [4, с. 1264–1269].

I шаг: построим статистический ряд для первичной обработки результатов исследования. Для этого построим статистический ряд (табл. 1), в 1-й строке располагая значение i – порядковый номер проводимого наблюдения (i - дискретная величина, принимающая значение от 1 до 50 включительно согласно условию задачи), во 2-й строке – соответствующее значение Хi (16, 14, 17, …).

Таблица 1.

Статистический ряд

II шаг: для того чтобы сделать определенные выводы о полученных результатах, построим простой вариационный ряд (табл. 2), указывая в 1-й строке значения Хi в порядке их количественного увеличения, во 2-й строке числа, указывающие, сколько раз было получено данное значение результата наблюдения. Очевидно, что для заполнения 1-й строки следует выделить неповторяющиеся значения результатов исследования и расположить их в порядке возрастания; при заполнении 2-й строки необходимо подсчитать, сколько раз встречается один и тот же результат наблюдения например, число 12 встречается 1 раз, число 13–3 раза, число 14–5 раз и т.д.).

Таблица 2.

Простой вариационный ряд

III шаг: для анализа полученных данных найдем относительную частоту каждого результата и построим расширенный вариационный ряд (табл. 3), отмечая в 1-й строке Хi , во 2-й строке – mi , в 3-й строке – vi , относительную частоту каждого результата, вычисляемую на основании данных 2-й строки табл.2, по формуле

vi = mi / n                                                               (1)

Например: vi (12) = mi (12) / n = 1 / 50 = 0,02 полученное значение заносим во 2-й столбец 3-й строки табл. 3; аналогично вычисляем частоты встречаемости для остальных значений Хi.

Таблица 3.

Расширенный вариационный ряд

IV шаг: наглядно представим закономерность распределения результатов наблюдений [1, с. 460]. Для этого построим полигон распределения частот на основе расширенного вариационного ряда (табл. 3). При этом по оси абсцисс будем откладывать значения результатов наблюдений Хi, по оси ординат – относительные частоты встречаемости vi каждого результата; полученные точки соединим ломаной линией (рис. 1).

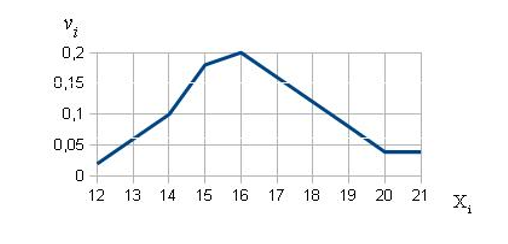
Рисунок 1. Полигон распределения частот

V шаг: в продолжение наглядного представления закономерности распределения результатов наблюдений составим интервальный вариационный ряд, объединяя имеющиеся значения Хi в несколько групп, называемых классами. Величина интервала, в пределах которого будут располагаться результаты исследования, относящиеся к одному и тому же классу, определяется по формуле

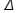Х = (Xmax - Xmin) / (1 + 3,32 ∙ lg n)                                   (2)

Получаем значение 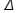Х = (21 – 12) / (1 + 3,32 ∙ lg 50) = 1,36

Учитывая, что исходные данные в задаче – дискретные величины, округляем величину интервала до целого значения: 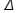Х ≈ 2. Далее необходимо определить нижнюю границу первого интервала по формуле Стерджесса:

X1 = Xmin- 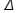Х / 2                                                         (3)

т.е. в нашей задаче X1 = 12 - 2 / 2 = 11 это значение, с которого начинается первый интервал. Следующий, второй интервал начнется со значения X2 = X1 + 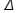Х = 11 + +2 = 13, третий интервал начнется со значения X3= X2+ 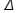Х = 13 + 2 = 15 и т.д.

Далее нужно определить, сколько результатов исследования попадает в каждый из классов, суммируя данные соответствующих столбцов 2-й строки табл. 3. Также для построения интервального вариационного ряда потребуется относительная частота попадания результатов измерений в i-й класс (группу), вычисляемая по формуле (1): например, для первого интервала v1 = m1 / n = 4 / 50 = 0,08. Аналогичный расчет проводится для других интервалов (табл. 4).

Таблица 4.

Интервальный вариационный ряд

VI шаг: представим результаты исследования на гистограмме (столбчатой диаграмме), откладывая по оси абсцисс границы интервалов (данные 1-й строки табл. 4), по оси ординат – значения относительных частот попадания результатов измерений в i-й класс; полученные точки соединим (рис. 2).

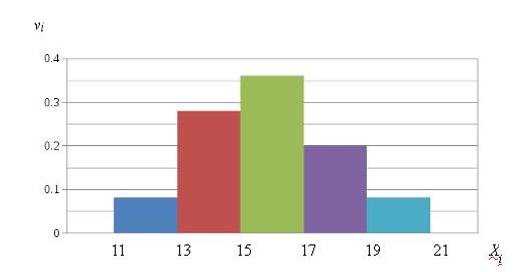
Рисунок 2. Гистограмма

Полигон распределений и гистограмма наглядно показывают, как часто встречаются те или иные значения исследуемого параметра, те или иные значения результатов опытов или измерений.

VII шаг: для наглядного представления статистических данных составим таблицу накопленных частот, откладывая в 1-й строке срединные значения классовых интервалов, во 2-й строке – значения накопленных частот, представляющие собой суммы частот предыдущих классов, начиная с первого. Пользуясь величинами, внесенными во 2-ю строку табл. 4, определим значения накопленных частот:

для первого интервала 0,08;

для второго интервала 0,08 + 0,28 = 0,36;

для третьего интервала 0,08 + 0,28 + 0,36 = 0,72;

для четвертого интервала 0,08 + 0,28 + 0,36 + 0,2 = 0,98;

для пятого интервала 0,08 + 0,28 + 0,36 + 0,2 + 0,08 = 1,0.

Эти значения заносятся во 2-ю строку таблицы накопленных частот (табл. 5).

Таблица 5.

Накопленные частоты

VIII шаг: на основании таблицы накопленных частот построим кумуляту, откладывая по оси абсцисс срединные значения классовых интервалов, а по оси ординат значения накопленных частот (рис. 3).

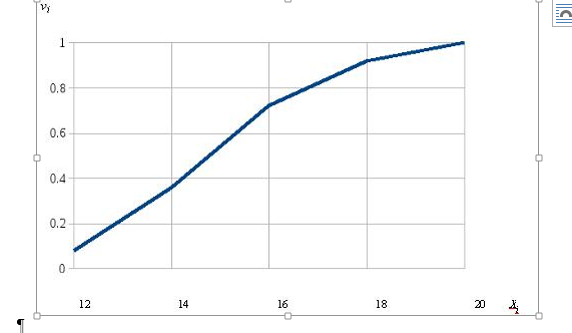
Рисунок 3. Кумулята

IX шаг: построим огиву (рис. 4), меняя оси местами по сравнению с кумулятой. При этом по оси абсцисс окажутся значения накопленных частот (данные 2-й строки табл. 5), по оси ординат - срединные значения классовых интервалов (данные 1-й строки табл. 5).

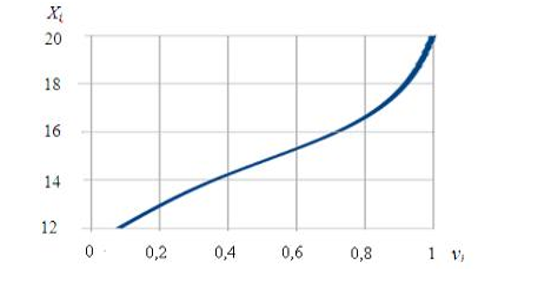
Рисунок 4. Огива

Особенность данной кривой в том, что она позволяет сравнивать между собой несколько статистических распределений разного объема для данной выборки [2].

На примере одной задачи нами рассмотрены различные виды статистических распределений и графического представления данных с помощью редактора электронных таблиц Excel. Показано, как формируется статистический ряд, простой и расширенный вариационные ряды, описана последовательность действий по построению графиков распределения частот, гистограммы, кумуляты, огивы.

Надеемся, что материалы статьи окажутся полезными для студентов медицинских ВУЗов, а также практикующих медработников при проведении статистической обработки данных. Представители иных сфер деятельности могут обрабатывать свои данные согласно приведенному образцу по аналогии.