Исследование масштабируемых алгоритмов анализа графов на основе фреймворка Apache Spark

Графовое представление данных является более выгодным, когда речь заходит о моделировании реальных данных, потому что оно интуитивно понятно, более гибкое чем таблицы и строки и потому, что алгоритмы, используемые при обработке графов, исследуются и дополняются уже долгое время. Как следствие, имеется несколько доступных графических баз данных, Neo4j является одной из самых известных.

То же самое касается обработки графов, алгоритмы многочисленны и понятны и имеют непосредственные приложения: кратчайший путь с одним источником, поиск маршрута, обнаружение цикла, поиск сообществ в графе. Spark GraphX поставляется с коллекцией таких алгоритмов, построенных в своем пакете.

Методы и алгоритмы теории графов активно используются в различных областях науки и техники. Один из данных алгоритмов: алгоритм Label Propagation, который чаще всего используется для поиска сообществ для дальнейшего исследования каждого из них.

Граф – абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин.

В жизни часто встречаются ситуации, отлично моделируемые с помощью графов. Графы могут быть очень разнообразны по своей структуре, и одними из часто встречаемых являются социальные графы.

Особенности социального графа характеризуются такими метриками, как: метрики взаимоотношений, метрики связей и сегментации. Для решения задач на социальном графе используются специальные модели, с помощью которых можно заменить «реальные» графы. С помощью социальных графов решают такие задачи, как: идентификация пользователей; социальный поиск; генерация рекомендаций по выбору «друзей», медиаконтента, новостей и тому подобного; выявление «реальных» связей или сбор открытой информации для моделирования графа.

Apache Spark GraphX – компонент Spark для вычислений над графами. GraphX расширяет стандартное базовое понятие устойчивого распределенного набора данных (RDD) представляя новую абстракцию: направленный мультиграф со свойствами, прикрепленными к каждой вершине и связи. GraphX содержит коллекцию алгоритмов над графами для упрочения задач анализа графов.

PageRank измеряет важность каждой вершины в графе, предполагая что связь между  и представляет собой подтверждение важности  над . Например, если на один сайт ссылаются множество других, то этот сайт получит более высокий ранг.

Допустим, что большинство соседей какой-либо вершины принадлежат одному сообществу. Тогда, с высокой вероятностью, ему также будет принадлежать выбранная вершина. На этом предположении и строится алгоритм Label Propagation: каждая вершина в графе определяется в то сообщество, которому принадлежит большинство его соседей. Если же таких сообществ несколько, то выбирается случайно одно из них.

В начальный момент времени всем вершинам ставится в соответствие отдельное сообщество. Затем происходят перераспределения сообществ. Из-за случайности важно на каждой итерации изменять порядок обхода вершин. Алгоритм заканчивает работу, когда нечего изменять: все вершины относятся к тем сообществам, что и большинство их соседей. Главное достоинство данного алгоритма — почти линейная сложность. Однако на зашумленных графах зачастую происходит объединение всех вершин в одно сообщество.

Данный алгоритм состоит из 5 шагов:

– Всем вершинам ставится в соответствие какое-либо сообщество

– Вводится переменная 

–  Все вершины перемешиваются в случайном порядке и присваиваются сообществу X

– Для каждой вершины , вводится функция , которая определяет принадлежность вершины к определенному сообществу в зависимости от сообщества соседей .

– Если все вершины принадлежат такому же  сообществу как и соседи, то алгоритм останавливается, иначе происходит присваивание  и возвращение к 3 шагу.

Для выполнения работы была использована база данных всех аудио и видео записей с TED Talks, доступных на сайте TED.com на момент 21 сентября 2017 года. Необходимо преобразовать базу так, чтобы избавится от излишней информации для представления графа в Neo4j. Каждая запись в графе содержит:

–  id: идентификатор выступления. Проставляется автоматически;

– name: официальное название выступления TED Talk. Содержит заголовок и имя автора;

– event: название мероприятия;

–  speaker: имя выступающего;

– title: заголовок выступления.

Вычисления производились при помощи фреймворка Apache Spark GraphFrame и графовой базы данных Neo4j.

Для начала работы необходимо записать данные из файла в котором распространяется данный набор данных в графовую базу данных Neo4j и выполнить запрос который создаст связь между выступлениями по их ссылкам на другие статьи. На рисунке 1 показана выборка из 300 объектов после создания связей в графе.

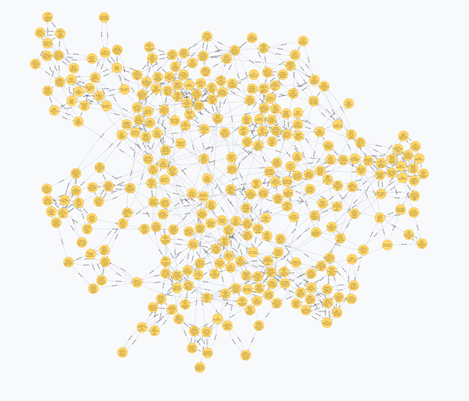
Рисунок 1. результат вывода 300 связанных объектов

После успешного создания графа можно использовать алгоритм Label Propagation для выделения сообществ. Для этого необходимо создать граф на основе фреймворка GraphFrame и применить к нему метод labelPropagation. Данный алгоритм принимает на вход вершины и ребра графа, а так же максимальное число итераций. Очевидно, что чем больше число итераций тем точнее будет результат алгоритма. Результат выполнения данного алгоритма показан на рисунке 2.

Рисунок 2 .результат анализа графа алгоритмом Label Propagation

После выполнения алгоритма, с помощью Neo4j Java Driver можно подключится к исходной и построить связи между соответствующими метками. Результат построения показан на рисунке 3.

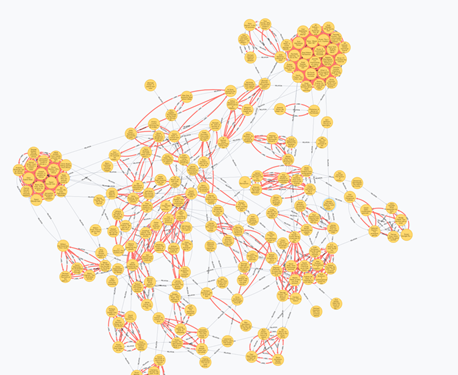
Рисунок 3. результат анализа графа

Видно, что с помощью данного метода образовались сообщества, которые тесно связанны друг с другом исходными ребрами графа.

Результат алгоритма можно изменить, если поменять параметр максимальных итераций для алгоритма. Соотношение количества итераций к затраченному времени показано в таблице 1.

Таблица 1.

Отношение количества итераций к затраченному времени

По таблице видно, что затраченное время выполнения алгоритма растет нелинейно. Для первой итерации необходимо загрузить граф в память и проставить индексы. Однако, уже после 5 итерации результат алгоритма не меняется.

Результат применения этой процедуры – ярлыки, то есть сообщества, к которым в конечном счёте отнесены вершины, могут немного различаться при нескольких попытках запуска этой процедуры. Это связано с тем, что процесс «распространения ярлыков» начинается каждый раз со случайным образом выбранных вершин (при условии, что мы не зафиксировали ни одной вершины). Иногда возможность получить несколько разных, но значимых решений может быть полезна, поскольку реальные сети с содержательной точки зрения могут иметь несколько приемлемых вариантов деления на сообщества (в этом случае можно говорить о пересекающихся сообществах). Конечно, это справедливо только при условии, что деление на сообщества будет эффективным (то есть что их будет относительно немного).