Системы массового обслуживания. Решение типичных задач

Введение

В экономическом моделировании существует множество теорий, согласно которым экономисты и математики рассчитывают характеристики систем для принятия определенных решений. Одна из таких теорий – теория систем массового обслуживания.

Системой массового обслуживания называют систему, в которой, с одной стороны, возникают массовые запросы (требования, заявки, транзакты) на выполнение каких-либо видов услуг, а с другой стороны, происходит удовлетворение этих запросов автоматами, работниками и т.п. (обслуживающими каналами, устройствами), имеющими ограниченные возможности обслуживания. Система массового обслуживания состоит из элементов: источник требований, входящий поток требований, очередь, обслуживающее устройство (обслуживающий аппарат, канал обслуживания), а также выходящий потом требований.

В данной статье рассматриваются наиболее типичные задачи на расчет характеристик систем массового обслуживания.

Задача №1

Одноканальная СМО с отказами представляет собой одну телефонную линию. Заявка (вызов), пришедшая в момент, когда линия занята, получает отказ. Все потоки событий простейшие. Интенсивность потока λ=0,95 вызова в минуту. Средняя продолжительность разговора t=1 мин. Определите вероятностные характеристики СМО в установившемся режиме работы. Сколько телефонов должно работать параллельно, чтобы вероятность отказа была меньше 1/10?

Решение

Определим исходные данные. Интенсивность входящего потока указана в условии и равна 0,95 вызова в минуту (λ=0,95). Интенсивность потока обслуживания µ=1/t=1/1=1 заявка в минуту. Система может находиться в одном из состояний: (1) S0 – телефонная линия свободна; (2) S1 – телефонная линия занята. Поток заявок переводит систему из состояния S0 в состояние S1 с интенсивностью λ=0,95, из состояния S1 в S0 с интенсивностью µ=1. Построим граф состояний системы (Рис. 1).

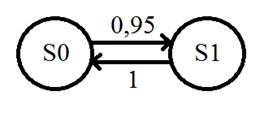
Рисунок 1. Задача 1. Граф состояний системы

Определим характеристики работы СМО в предельном режиме.

 – вероятность того, что система свободна (телефонная линия свободна, заявок нет).

 – вероятность того, что заявка в системе (телефонная линия занята). Этот же показатель – вероятность отказала в обслуживании.

– относительная пропускная способность.

 – абсолютная пропускная способность. Среднее число заявок, обслуживаемых в минуту.

 – среднее время обслуживания заявки.

 – среднее время простоя канала (телефонной линии).

 – среднее время пребывания заявки в системе.

Теперь необходимо определить, сколько телефонов должно работать параллельно, чтобы вероятность отказа была меньше 1/10, т.е. определить количество каналов k для условия  .

Предположим, что k=2.

 – приведенная интенсивность входящего потока.

Вероятность отказа – 0,188 – больше, чем требовалось. Значит, двух каналов будет недостаточно для того, чтобы вероятность отказа была меньше 0,1. Попробуем предположить, что k=3, и подсчитать те же показатели.

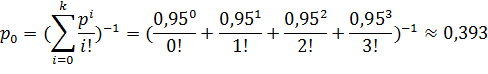
Интерпретация результатов

Вероятность отказа при трех каналах равна 0,056<0,1, а значит, трех каналов будет достаточно для того, чтобы вероятность отказа была меньше 0,1.

Задача №2

В вычислительном центре работает 5 персональных компьютеров (ПК). Простейший поток задач, поступающих на ВЦ, имеет интенсивность λ=10 задач в час. Среднее время решения задачи равно 12 мин. Заявка получает отказ, если все ПК заняты. Найдите вероятностные характеристики системы обслуживания (ВЦ).

Решение

Определим исходные данные. Интенсивность входящего потока λ=10 задач в час=10/60=1/6 в минуту. Среднее время обслуживания (решения задачи) t – 12 мин, значит интенсивность потока обслуживания . Число каналов n=5. Система имеет следующие состояния: (1) S0 – компьютеры свободны; (2) S1 – 1 компьютер занят, остальные свободны; (3) S2 – 2 компьютера заняты, остальные свободны; (4) S3 – 3 компьютера заняты, остальные свободны; (5) S4 – 4 компьютера заняты, остальной свободен; (6) S5 – все компьютеры заняты. Построим граф состояний (Рис. 2).

Рисунок 2. Задача 2. Граф состояний системы

Система переходит из любого левого состояния в следующее правое с интенсивностью 1/6. Интенсивность перехода из правого в левое состояние меняется в зависимости от состояния. Например, из состояния S2 (2 компьютера заняты) в S1 (один компьютер занят) система может перейти тогда, когда закончит работу либо второй, либо первый компьютер, то есть суммарная интенсивность их потоков обслуживания будет 2µ = 2/12.

Определим приведенную интенсивность входящего потока: .

.

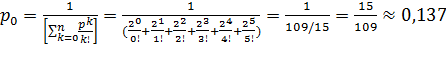Предельные вероятности состояний найдем по формулам Эрланга:

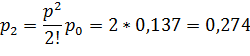
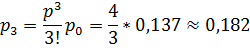
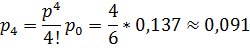
– вероятность отказа в обслуживании заявки.

 – относительная пропускная способность системы (ВЦ).

 – абсолютная пропускная способность системы (ВЦ).

 – среднее число занятых каналов.

Интерпретация результатов

Из вычисленных показателей видно, что в установившемся режиме работы системы в среднем будут заняты 2 канала (ПК) из 5, а остальные 3 будут простаивать. Вероятность отказа в обслуживании в среднем 3-4%, а значит, работу системы можно считать удовлетворительной.

Задача №3

На пункт техосмотра поступает простейший поток заявок (автомобилей) интенсивности λ=4 машины в час. Время осмотра распределено по показательному закону и равно в среднем 17 мин., в очереди может находиться не более 5 автомобилей. Определите вероятностные характеристики пункта техосмотра в установившемся режиме.

Решение

Определим исходные данные. Интенсивность входящего потока λ=4 машины в час=4/60=1/15 в минуту. Среднее время обслуживания t=17 мин, значит интенсивность потока обслуживания µ=1/t=1/17. Число каналов n=1. Число мест в очереди m=5.

Определим приведенную интенсивность входящего потока:

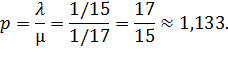
N = n+1 = 6 – очередь и обслуживаемый в данный момент клиент.

Вычислим вероятности нахождения заявок в системе:

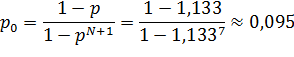
 – вероятность отказа в обслуживании.

 – относительная пропускная способность системы (пункта техосмотра).

 – абсолютная пропускная способность системы.

 – среднее число занятых каналов.

Среднее число находящихся в системе заявок (в очереди и на обслуживании):

Среднее время пребывания заявки в системе:

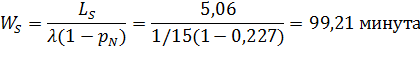
Средняя продолжительность пребывания заявки в очереди на обслуживание:

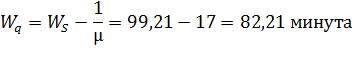
Среднее число заявок в очереди (длина очереди):

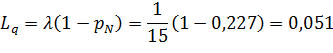
Интерпретация результатов

Таким образом, работу пункта техосмотра нельзя считать удовлетворительной, так как ему приходится отказывать в обслуживании автомобилей в среднем в 22,7% случаев, при этом в среднем клиентам будет приходиться находиться в очереди около 1,2 часа.

Задача №4

На промышленном предприятии решается вопрос о том, сколько потребуется механиков для работы в ремонтном цехе. Пусть предприятие имеет 10 машин, требующих ремонта с учетом числа ремонтирующихся. Отказы машин происходят с частотой λ=10 отк/час. Для устранения неисправности механику требуется в среднем t=3 мин. Распределение моментов возникновения отказов является пуассоновским, а продолжительность выполнения ремонтных работ распределена экспоненциально. Возможно организовать 4 или 6 рабочих мест в цехе для механиков предприятия. Необходимо выбрать наиболее эффективный вариант обеспечения ремонтного цеха рабочими местами для механиков.

Решение

Определим исходные данные. Интенсивность входящего потока λ=10 отк/час=10/60=1/6 в минуту. Интенсивность потока обслуживания µ=1/t=1/3.

N=10.

Рассмотрим вероятность отказа в обслуживании для n=4 и n=6 рабочих мест в цехе для механиков (n – число каналов обслуживания).

n=4

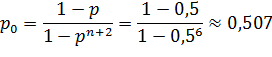
n=6

Интерпретация результатов

Таким образом, вероятность отказа в обслуживании практически равна нулю во втором случае (6 рабочих), поэтому если это принципиально, то лучше иметь 6 рабочих.