Визуализация и отображение графов на плоскости

Аннотация. Визуализация или отображение графов, относящееся к топологии и геометрии – двумерное представление графа. В основном, это графическое представление укладки графа на плоскость, направленное на более удобное отображение некоторых свойств графа или модулируемого объекта.

Ключевые слова: силовой алгоритм, визуализация графов, изображение графа на плоскости.

Цели и Задачи:

Целью данной работы является реализация и исследование силового алгоритма визуализации графов.

• Реализация представления структуры графов и алгоритмов визуализации;
• Реализация методов позволяющих узнать дополнительную информацию о графе, в частности поиск радиуса и центра;
• Найти практическое применение для такого вида разработки.

Построение маршрутов и поиск кратчайшего пути:

Одной из проблем, которую могут решить графы является поиск кратчайшего пути, с этой задачей легко справляются алгоритмы обхода графов и поиск кратчайшего пути.

Для представления информации:

Графы применяются для представления любой информации, которую можно промоделировать в виде объектов и связей между объектами. Поэтому визуализация графовых моделей является ключевой компонентой во многих приложениях в науке и технике, а методы визуализации графов представляют собой теоретическую основу методов визуализации абстрактной информации.

Для получения необходимых признаков:

Несмотря на то, что алгоритмы визуализации графов в основном разрабатывались только как инструменты для получения конкретных изображений, их можно применять в качестве методов снижения размерности. Сам по себе граф, если представить его матрицей смежности – это данные в пространстве высокой размерности, а при визуализации мы получаем две координаты для каждой вершины (бывают исключительные ситуации, когда три и более, но такие случаи крайне редкие).

Основные способы укладки графов:

-Force-directed and Energy Based

-Dimension Reduction

-Feature-Based Layout

В контексте данной работы будет рассмотрен Force-directed алгоритм, а именно алгоритм Frushterman-Reingold.

Алгоритм «Frushterman-Reingold»:

Алгоритмы на основе физической модели в своей основе имеют соответствие некоторой физической модели. Рассмотрим более подробно Алгоритм «Frushterman-Reingold» был разработан в 1991 году Томасом Фруштерманом и Эдвардом Рейнгольдом (Фруштерман и Рейнгольд, 1991). Сложность алгоритма O (N^2). Он позволяет эффективно строить двумерные представления графов, в которых содержится не более 1000 вершин. Силовые алгоритмы визуализации графов назначают силы на множестве рёбер и узлов графа. Обычно используются подобные пружинным силы притяжения на основе закона Гука формула (1) для назначения сил парам концов ребра графа.

,                                                                                                              (1)

где     – постоянная величина;

 – удлинение тела, м.

В контексте рассматриваемой работы величина  будет характеризовать разницу между длинной пружины и расстоянием между узлами (удлинение пружины).

В то же время используются силы отталкивания, подобные отталкиванию электрических заряженных частиц на основе закона Кулона формула (2)

,                                                                                                             (2)

где     – постоянная величина;

 – заряд, Кл;

r – расстояние между частицами, м.

Сила отталкивания прилагается к каждому узлу к графе, и каждый узел отталкивается (хотя и незначительно) всеми остальными узлами в графе. Поскольку в данной работе все узлы эквивалентны, мы можем игнорировать термин заряда. Другими словами, по мере увеличения расстояния между узлами сила отталкивания уменьшается квадратично. Для получения равновесного состояния этой системы сил, ребра стремятся получить однородные длины (ввиду действия пружин), а узлы, не связные ребром, стремятся расположиться поодаль друг от друга (ввиду действия сил отталкивания). Силы притяжения (рёбра) и силы отталкивания (узлы) могут быть определены с помощью функций, которые не основаны на физическом поведении пружин и частиц.

Алгоритм визуализации графа:

Основной алгоритм разрабатываемой программы основан на прототипе физической модели. Узлы графа представлены, как точки на плоскости, которые электрически заряжены и взаимодействуют друг с другом посредством силы отталкивания. Ребра, соединяющие данные точки, имитируя силу упругости, притягивают соседние узлы. Модель итеративно определяет результирующие силы, которые действуют на узлы, и пытается переместить узлы в положение равновесия. Когда все силы в сумме равны нулю, а положение узлов остается стабильным алгоритм заканчивает свою работу.

1) Введем матрицу смежности вручную и посмотрим на полученный результат. Для удобного отображения результата откроем приложение в оконном режиме, введенной матрицы смежности изобразим её в виде таблицы 1. А полученный результат в виде рисунка 1.

Таблица 1.

Введенная вручную матрица смежности

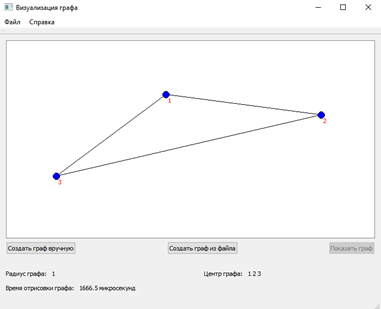
Рисунок 1. Результат работы программы

2) Повторим тестирование, на этот раз изменим способ создания графа и считаем матрицу смежности из файла.

Тогда результатом выполнения программы будет граф, изображенный на рисунке 2.

Рисунок 2. Результат работы программы

3) Увеличим число заданных вершин. В качестве примера рассмотрим граф состоящий из 10 вершин. На рисунке 4 представлен граф, полученный в результате работы алгоритма программы.

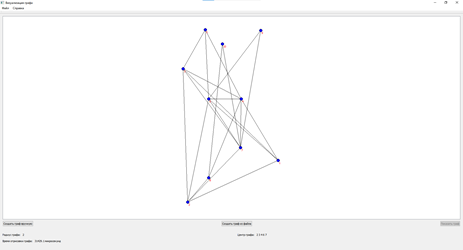
Рисунок 3. Результат визуализации графа на 10 вершинах

Вывод:

Таким образом, в данной работе был рассмотрен силовой алгоритм укладки графа на плоскости и на его основе создана программа для работы с графами, которая дает возможность пользователю с помощью матрицы смежности создавать граф и визуализировать его на плоскости, при этом автоматически определять радиус и центры графа. Помимо этого, в функционал данной программы входит отслеживание времени визуализации графа, которое можно использовать для проведения исследовательской работы.