МЕТРИЧЕСКИЕ ЗАДАЧИ С ПОЗИЦИЙ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

Аналитическая геометрия - раздел геометрии, который исследует простейшие геометрические объекты средствами элементарной алгебры на основе метода координат. Основная задача аналитической геометрии заключается в изучении геометрических фигур с помощью соотношений между координатами точек, из которых эти фигуры образованы.

Начертательная геометрия – раздел геометрии, в котором пространственные фигуры изучаются при помощи построения их изображений на плоскости, в частности построения проекционных изображений, а также методы решения и исследования пространственных задач на плоскости.

Цель начертательной геометрии – развитие пространственного представления и воображения, конструктивно-геометрического мышления, способности к анализу и синтезу пространственных форм и отношений на основе графических моделей пространства, практически реализуемых в виде чертежей конкретных пространственных объектов и зависимостей.

Задача изучения начертательной геометрии сводится к изучению способов получения определенных графических моделей пространства, основанных на ортогональном проецировании и умении решать на этих моделях задачи, связанные пространственными формами и отношениями.

Рассмотрим на примерах метрических задач связь аналитической и начертательной геометрии.

Метрическими называются задачи, решение которых связано с нахождением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами.

Все метрические задачи, в итоге, сводятся к решению двух задач, которые называются основными метрическими задачами:

1.  Первая основная метрическая задача - построение угла между прямой и плоскостью.

2.  Вторая основная метрическая задача – определение расстояния между двумя точками.

В данной статье рассмотрим построение прямого угла с аналитической точки зрения.

1.  Перпендикулярность прямых в плоскости.

Две прямые на плоскости перпендикулярны, если при пересечении образуют 4 прямых угла.

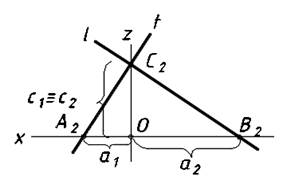
Рисунок 1. Перпендикулярность двух прямых

В плоскости проекций П₂ заданы две перпендикулярные прямые l и t (рис.1).

Из подобия треугольников С₂ОА₂ и В₂ОС₂ следует:

a₁/c₁ = a₂/c₂ или

a₁/c₁ - a₂/c₂ =0.                                                               (1)

Формула (1) является аналитическим выражением перпендикулярности двух прямых в плоскости.

2.  Перпендикулярность прямой и плоскости.

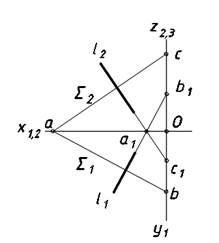
Рисунок 2. Перпендикулярность прямой и плоскости

Из курса стереометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна хотя бы к двум пересекающимся прямым, принадлежащим этой плоскости.

Дана прямая l перпендикулярная плоскости S, заданной следами (рис.2).

Плоскость S задана уравнением:

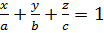                                               (2)

Прямая проходит через две точки с координатами (а₁, 0,0) и (0, - b_1, -c₁). В соответствии с

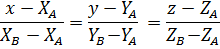
получим уравнение прямой l:

x/ а₁=(y+ b₁)/ b₁=(z+ c₁)/ c₁                                         (3)

или:

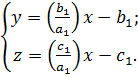                                                 (4)

Из подобия треугольников Оас и Оа₁с₁ следует:

a/c=c₁a₁ или aa₁=cc_1.

Из подобия треугольников Оаb и Оа₁b₁ следует:

a/b=b₁a₁ или aa₁=bb_1.

Окончательно:

aa₁= bb₁=cc_1.                                                                 (5)

Полученное выражение является условием перпендикулярности прямой и плоскости.

3.  Перпендикулярность двух прямых в пространстве.

Прямые перпендикулярны, если через одну из прямых можно провести плоскость, перпендикулярную к другой прямой.

Допустим: прямая l проходит через две точки 1(X₁;Y₁;Z₁) и 2(X₂;Y₂;Z₂);

 прямая t через две точки 3(X₃;Y₃;Z₃) и 4(X₄;Y₄;Z₄).

Представим прямую l аналитически:

.

Таким образом, сравнивая

и x/ а₁=(y+ b₁)/ b₁=(z+ c₁)/ c₁ получим для прямой l:

a=X₂ – X₁;

b=Y₂ – Y₁;

c=Z₂ – Z₁.

Заключим прямую t в плоскость:

A(X₄-X₃) +B (Y₄-Y₃) +C (Z₄-Z₃) =0.                      (6)

Если прямые l и t перпендикулярны, то выполняется условие перпендикулярности прямой и плоскости:

a₁/A=b₁/B=c₁/C                                                    (7)

или (X₂-X₁)/A = (Y₂-Y₁)/B = (Z₂-Z₁)/C

Отсюда A=B(X₂-X₁)/ (Y₂-Y₁), и C= B(Z₂-Z₁)/ (Y₂-Y₁).

Подставив эти выражения в (7) и умножив каждый член на (Y₂-Y₁)/B, получим аналитическое условие перпендикулярности прямых.

(X₂-X₁) (X₄-X₃)+ (Y₂-Y₁) (Y₄-Y₃) + (Z₂-Z₁) (Z₄-Z₃)=0 (8).

4.  Перпендикулярность двух плоскостей.

Плоскости перпендикулярны, если одна из них содержит прямую перпендикулярную другой плоскости.

Заданы две плоскости:

S: A₁X + B₁Y + C₁Z + D₁=0;

D: A₂X + B₂Y + C₂Z + D₂=0.

Допустим, что прямая l проходит через две точки 1(X₁;Y₁;Z₁) и 2(X₂;Y₂;Z₂) плоскости S. Условие принадлежности прямой l плоскости S:

A₁(X₂-X₁)+B₁(Y₂-Y₁)+C₁(Z₂-Z₁)=0.                        (9)

Отсюда перпендикулярность прямой l и плоскости D, принимая в расчет (7) выразиться:

(X₂-X₁)/ A₂+(Y₂-Y₁)/ B₂+(Z₂-Z₁)/ C₂

или (X₂-X₁)= A₂(Y₂-Y₁)/ B₂;

(Z₂-Z₁)= C₂(Y₂-Y₁)/ B₂.

Подставляя полученные выражения в () и деля все члены на (Y₂-Y₁)/ B₂,

окончательно получим условие перпендикулярности двух плоскостей:

A₁A₂= B₁B₂= C₁C₂=0.                                 (10)

В отличие от аналитических определения метрических характеристик, геометрические решения довольно-таки приблизительны, хотя с математической точки зрения, являются геометрически точными.

Список литературы:

1. Бугров Я.С., Никольский СМ. Высшая математика. Элементы ли­нейной алгебры и аналитической геометрии: учеб. для вузов. - М.: Наука, 1988. – 224 с.

2. Бубенников А.В. Начертательная геометрия: учебник для втузов/ А.В. Бубенников. – 3-е изд., перераб. и доп. – М.: Высшая школа, 1985. – 288 с.

3. Феоктистова Л.А., Талипова И.П., Рзаева Т.В. К вопросу о связи начертательной геометрии с аналитической геометрией. Естественные и технические науки. - Москва: Изд-во Спутник +, 2015. - №11 - С. 303–307