Моделирование процесса температуропроводности в тонкой прямоугольной пластине

В данной работе в качестве объекта исследования рассматривается квадратная пластина со стороной равной 1. Полагается также, что процесс температуропроводности описывается однородным уравнением с коэффициентом a=1:

u'_t - ( u"_xx + u"_yy ) = 0.

Начальная температура пластины: u(x,y,0)=0, т.е. температура внутри тела (за исключением границы) везде равна 0. Длина каждого участка изоляции, заданной на границе, равна 0,5.

Граничные условия:

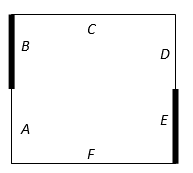
·     Участок A: .

·     Участок B: теплоизоляция.

·     Участок C: .

·     Участок D: .

·     Участок E: теплоизоляция.

·     Участок F: .

Положим, что процесс температуропроводности внутри пластины описывается однородным дифференциальным уравнением, с коэффициентом a=1[1]:

u'_t - ( u"_xx + u"_yy ) = 0.

Положим также, что температура вдоль границ пластины B, E со временем не меняется (статична), а значения температуры вдоль остальных границ образуются граничными условиями 1 рода:

·     Сторона A: .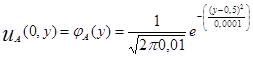

·     Сторона F:

·     Сторона D:

·     Сторона C: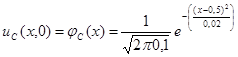  

Пусть на границе B присутствует термоизоляция. Угол α отклонения нормали  к границе B от оси x равен π. Тогда угол β отклонения нормали от оси y будет равен  - π = . Тогда граничное условие термоизоляция (условие 2-го рода) будет иметь вид:

·     Сторона B: .

·     Сторона E:

В качестве начальных условий положим, что при t=0 температура внутри пластины во всех точках равна 0:

·     ,

т.е. температура внутри тела (за исключением границы) везде равна 0.

Приведённое описание предмета моделирования не даёт оснований для введения условий 3-го рода.

Для исследования динамики температуропроводности внутри пластины найдём решение дифференциального уравнения методом конечных разностей. Для этого заменим все дифференциальные уравнения конечно-разностными аналогами.

Поскольку пластина квадратная, то шаги дискретизации выберем одинаковые по x и y, т.е. h_x=h_y=h , следовательно l=h_x/h_y=1. Так как сторона квадрата равна 1, то h=1/n, n – количество делений дискретизации. Тогда шаг дискретизации по времени будет равен t = mh².

Конечно-разностная форма однородного дифференциального уравнения в данном случае примет вид:

.

Конечно-разностное уравнение граничного условия термоизоляции на границах B и E получим из полученного выше соотношения:

,

,

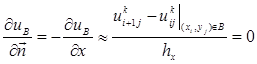откуда следует, что на границах B и E соответственно:

, "k=0,1,2,…

, "k=0,1,2,…

Построим теперь начальную матрицу температур тела 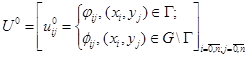 для n=10, используя ранее полученные

уравнения граничных и начальных условий. Вид матрицы U⁰ приведен на рисунке 1.

Рисунок 1. Результаты вычислений в графической форме

«Внутренние» элементы матрицы отражают начальное условие и будут равны 0. Первая строка матрицы будет соответствовать температуре на границе A и условию термоизоляции на границе B. Температура на границе B соответствует температуре в ближайших внутренних точках, т.е. равна 0. Первый столбец матрицы будет соответствовать температуре на границе C. Последняя строка матрицы будет соответствовать температуре на границе D и условию термоизоляции на границе E, а последний столбец – на границе F.

Полученная матрица определяет температуру в точках пластины в нулевой момент времени (начальный временной слой). Следующие временные слои вычисляются уже с использованием полученных выше зависимостей.

Рисунок 2. Результаты вычислений в матричной форме

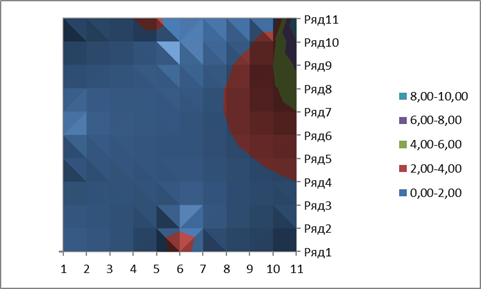
Рисунок 3. Результаты вычислений в графической форме

Исходя из проведенных исследований, можно сделать вывод, что на точность прогноза влияет не только предельное эвклидово расстояние между входным вектором и центром кластера и размер обучающей выборки, но также и размер плавающего окна. Наилучшие результаты по прогнозу дают обучающая выборка размером 240, предельное евклидово расстояние равное 0,005 и размер плавающего окна, равный 3.

Список литературы:

1.  Баландин А. В. Моделирование процесса температуропроводности в тонкой прямоугольной пластине. Методические указания. [Текст]. – Самара: СГАУ, 2014. – 27 с.