Методические фрагменты конспектов с использование компьютерной среды GeoGebra при изучении тригонометрии
Секция: Физико-математические науки
лауреатов
участников
лауреатов


участников



XII Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Методические фрагменты конспектов с использование компьютерной среды GeoGebra при изучении тригонометрии
Аннотация. В статье рассматриваются методические фрагменты конспектов, в которых используются анимационных возможностей компьютерной системы GeoGebra. Представлен опыт использования анимационных возможностей компьютерной системы GeoGebra в процессе изучения преобразования тригонометрических функций.
Ключевые слова. Компьютерная система GeoGebra, анимационные возможности, обучение тригонометрии, графики тригонометрических функций, преобразование, фрагменты уроков.
Сопровождение занятий по математике компьютерными имитационными моделями и интерактивными иллюстрациями (анимационные чертежи, «живые» рисунки) значительно облегчает проникновение в сущность математических понятий.
Анимационные чертежи можно использовать на разных стадиях изучения материала: как готовые наглядные пособия при изучении нового, как источник задач и сопровождения их решений, как инструмент для экспериментирования и проведения научных исследований. Попутно ученик учится использованию компьютерных технологий не только в обучении, но и при решении исследовательских задач [Ларин, 2015].
Рассмотрим фрагмент урока по теме «Преобразование графиков тригонометрических функций». Учащимся предлагается провести исследование и разделится на 4 группы. Занятие проходит за компьютером.
Задание для группы №1: C помощью компьютерной среды GeoGebra
-
постройте графики функций: y =
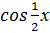 , y = cos 2x, y = cosx;
, y = cos 2x, y = cosx; - определите изменение графика в зависимости от изменения его аргумента.
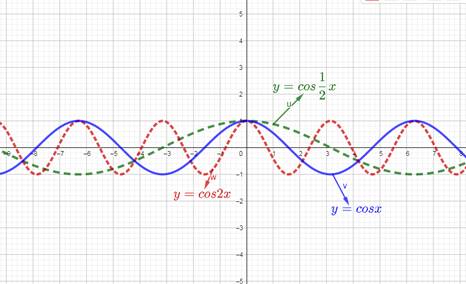
Рисунок 1. Математическая модель построенная для задания 1 группы
Задание для группы №2: C помощью компьютерной среды GeoGebra
- постройте графики функций: y = sinx; y = sin(x + 2); y = sin(x – 2);
- определите изменение графика в зависимости от изменения его аргумента.
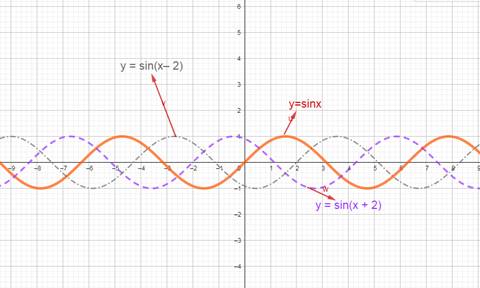
Рисунок 2. Математическая модель построенная для задания 2 группы
Задание для группы №3: C помощью компьютерной среды GeoGebra
-
постройте графики функций: y = cosx, y = 2cosx, y =
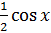 , y=-cosx
, y=-cosx - определите изменение графика в зависимости от изменения его аргумента.

Рисунок 3. Математическая модель построенная для задания 3 группы
Задание для группы №4: C помощью компьютерной среды GeoGebra
- постройте графики функций: y = sinx; y = sinx + 2; y = sinx – 2;
- определите изменение графика в зависимости от изменения его аргумента.

Рисунок 4. Математическая модель построенная для задания 4 группы
По завершению работы, каждая группа делает небольшое выступление об изменении графиков, затем совместно с детьми выделяются свойства графиков тригонометрических функций.

