Нахождение минимального остовного дерева
Конференция: XLVI Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Физико-математические науки

XLVI Студенческая международная научно-практическая конференция «Молодежный научный форум»
Нахождение минимального остовного дерева
Введение
В наше время всё чаще создаются проекты, в которых необходимо создание большой связанной сети, например, дорожной или телефонной. Для того, чтобы создать такую сеть на минимальное количество средств, используются алгоритмы нахождения минимального остовного дерева. Минимальное остовное (покрывающее) дерево – это остовное дерево графа, имеющее минимальный возможный вес, где вес дерева – это сумма весов входящих в него рёбер. Минимальный остов строится пошагово. Введем понятие промежуточного остовного леса. Промежуточный остовной лес – это такой подграф ![]() исходного графа
исходного графа ![]() , который удовлетворяет условию
, который удовлетворяет условию ![]() , где
, где ![]() – минимальный остов. На первом шаге
– минимальный остов. На первом шаге ![]() состоит из
состоит из ![]() отдельных вершин, компонент связности, не соединенных друг с другом ребрами. Новое добавляемое ребро
отдельных вершин, компонент связности, не соединенных друг с другом ребрами. Новое добавляемое ребро ![]() добавляется таким образом, чтобы выполнялось условие
добавляется таким образом, чтобы выполнялось условие ![]() и такое ребро называется безопасным. Безопасным ребром
и такое ребро называется безопасным. Безопасным ребром ![]() относительно некоторой компоненты связности
относительно некоторой компоненты связности ![]() назовем ребро с минимальным весом, ровно один конец которого лежит в
назовем ребро с минимальным весом, ровно один конец которого лежит в ![]() . Основными алгоритмами поиска минимального покрывающего дерева являются алгоритм Крускала и Прима. Данные алгоритмы могут быть применимы в:
. Основными алгоритмами поиска минимального покрывающего дерева являются алгоритм Крускала и Прима. Данные алгоритмы могут быть применимы в:
1. Разработке сетей;
2. Производстве печатных плат (соединить большое количество контактов с минимальной стоимостью операции);
3. Биологии (используются многомерные данные для группировки объектов, растений, животных).
Каждый из алгоритмов построен на выборе оптимального значения на каждом шаге выполнения. Пусть дан граф ![]() с
с ![]() вершинами и весовой функцией
вершинами и весовой функцией ![]() .
.
Постановка задачи.
Пусть имеется ![]() нефтезаводов, которые нужно объединить в единую нефтяную сеть. Для этого достаточно проложить
нефтезаводов, которые нужно объединить в единую нефтяную сеть. Для этого достаточно проложить ![]() трубопроводов между заводами. Необходимо соединить заводы так, чтобы суммарная длина труб была минимальна и создать программу, позволяющую решить данную задачу.
трубопроводов между заводами. Необходимо соединить заводы так, чтобы суммарная длина труб была минимальна и создать программу, позволяющую решить данную задачу.
В общем случае задача может быть сформулирована так. Пусть ![]() – связный неориентированный взвешенный граф где
– связный неориентированный взвешенный граф где ![]() – множество вершин,
– множество вершин, ![]() – множество ребер. Для каждого ребра
– множество ребер. Для каждого ребра ![]() определена весовая функция
определена весовая функция ![]() . Задача состоит в нахождении такого связного ациклического подграфа
. Задача состоит в нахождении такого связного ациклического подграфа ![]() удовлетворяющего условиям:
удовлетворяющего условиям:
1. ![]()
2. ![]()
Алгоритм Крускала.
Алгоритм Крускала работает следующим образом:
1. Алгоритм объединяет вершины графа в несколько связных компонент. Каждая компонента является деревом.
2. На каждом следующем шаге из всех ребер, которые соединяют вершины из различных компонент связности, выбирается ребро с наименьшим весом оно и является безопасным.
3. Добавляем выбранное ребро, если его концы лежат в разных компонентах связности.
|
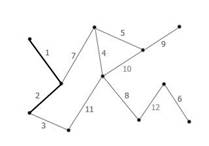
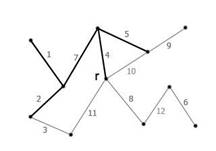
Рисунок 1. Начальная фаза. Минимальный покрывающий лес пуст. |
Рисунок 2.Перебираем ребра в порядке возрастания веса. Добавляем ребро с весом 1. |
Рисунок 3.Следующим добавляем ребро с весом 2. |
|
|
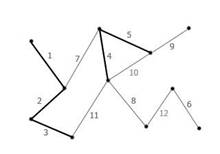
Рисунок 4. Ребра графа
|
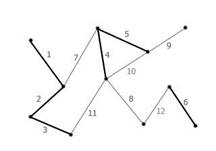
Рисунок 5 Ребра графа
|
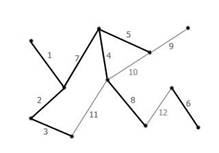
Рисунок 6 Ребра графа
|
|
|
Рисунок 7 Ребра графа
|
Рисунок 8 Ребра графа
|
Рисунок 9 Ребра графа
|
|
|
Рисунок 10 Ребра графа
|
Рисунок 11 - Минимальное остовное дерево построено |
||
При реализации графа для непересекающихся множеств воспользуемся двоичной кучей или очередью с приоритетами. Заполним её всеми ребрами графа. На каждом шаге будем доставать по одному ребру и объединять классы смежности, которые соединяет это ребро.
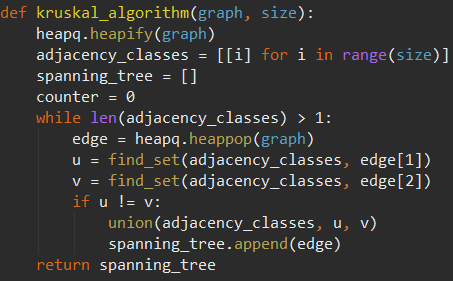
Рисунок 12 . Реализация алгоритма Крускала
![]() возвращает множество, содержащее данную вершину, а объединяет множества, содержащие данные вершины,
возвращает множество, содержащее данную вершину, а объединяет множества, содержащие данные вершины, ![]()
Сортировка ![]() займет
займет ![]() времени при использовании кучи. Работа с СНМ займет
времени при использовании кучи. Работа с СНМ займет ![]() , где
, где ![]() — обратная функция Аккермана, которая не превосходит 4 во всех практических приложениях и которую можно принять за константу. Алгоритм работает за
— обратная функция Аккермана, которая не превосходит 4 во всех практических приложениях и которую можно принять за константу. Алгоритм работает за ![]() .
.
Алгоритм Прима.
Рассмотрим работу алгоритма. Пусть у нас есть промежуточный остовной лес ![]() для графа
для графа ![]() . На первом шаге
. На первом шаге ![]() состоит только из одной вершины, называемой корень. На каждом следующем шаге добавляется новое безопасное ребро и существует не более одной нетривиальной компоненты связности. К ней добавляется ребро наименьшего веса, соединяющее вершины компоненты с остальными вершинами. Алгоритм работает за
состоит только из одной вершины, называемой корень. На каждом следующем шаге добавляется новое безопасное ребро и существует не более одной нетривиальной компоненты связности. К ней добавляется ребро наименьшего веса, соединяющее вершины компоненты с остальными вершинами. Алгоритм работает за ![]() шагов.
шагов.
|
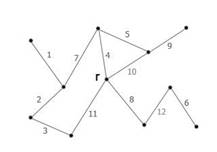
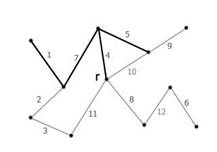
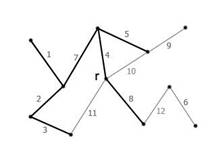
Рисунок 13 – Начальная фаза. Минимальный покрывающий лес состоит из корня и пустого множества ребер |
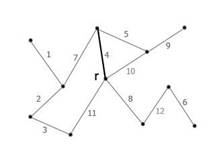
Рисунок 14 - Ребро с весом 4 является минимальным ребром, соединяющим корень с остальными вершинами. Добавляем его к минимальному остову. |
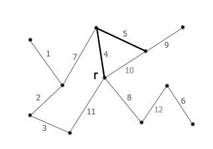
Рисунок 15 – Следующее безопасное ребро с весом 5. |
|
|
Рисунок 16 Ребра графа
|
Рисунок 17 Ребра графа
|
Рисунок 18 Ребра графа
|
|
|
Рисунок 19 Ребра графа
|
Рисунок 20 Ребра графа
|
Рисунок 21 Ребра графа
|
|
|
Рисунок 22 Ребра графа
|
Рисунок 23 Ребра графа
|
||
Для реализации алгоритма воспользуемся двоичной кучей. На вход алгоритма поступает граф ![]() и его корень
и его корень ![]() – начальная вершина для минимального остова. На первом шаге заполним кучу всеми ребрами исходящими из корня. На каждом последующем шаге будем вынимать безопасное ребро E(u, v) и добавлять в кучу ребра E(v, w). Выполняем n-1 раз.
– начальная вершина для минимального остова. На первом шаге заполним кучу всеми ребрами исходящими из корня. На каждом последующем шаге будем вынимать безопасное ребро E(u, v) и добавлять в кучу ребра E(v, w). Выполняем n-1 раз.

Рисунок 24. Реализация алгоритма Прима
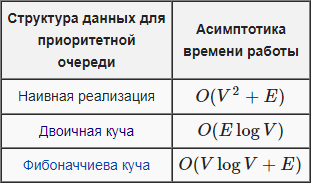
Производительность алгоритма Прима зависит от выбранной реализации приоритетной очереди (см. таблица 1).
Таблица 1.
Зависимость производительности алгоритма Прима от реализации приоритетной очереди
Заключение
Во время выполнения данной работы была создана программа, позволяющая находить минимальное остовное дерево. Программа успешно прошла все тесты. Время работы алгоритмов указано ниже (см. рисунок 25).

Рисунок 25. Время работы алгоритмов Прима и Крускала
Исходя из графика видно, что алгоритм Прима уступает в производительности при большом количестве вершин, однако это следует из недостатка определения оценки скорости. О символика скрывает любые константы т.к они считаются много меньше n. Алгоритм Прима в данном случае имеет большую константу нежели алгоритм Крускала.