АЗЫ ЧПУ. МАТЕМАТИКА И ГЕОМЕТРИЯ

«Геометрическая задача –это взаимодействие ЧПУ со станком для управления формообразованием детали. Решение данной задачи заключается в отображении геометрической информации чертежа». Далее необходимо следить за тем, чтобы чертеж превратился в готовое изделие [5].«Интерполяция –это вычислительный процесс в устройстве ЧПУ, обеспечивающий переход от укрупненного описания заданного перемещения к оперативным командам в функции времени для исполнительных приводов» [6].«Управляющая программа обработки детали представляет собой траекторию движения центра фрезы. Траектория движения состоит из отдельных, соединяющихся друг с другом участков, линейных или дуговых. Точки, которые задают траекторию, называются опорными. В действительности управляющая программа –это последовательный набор опорных точек». «Опорные точки могут лежать в плоскости, тогда для их задания используется две координаты –это двух координатная обработка. Другой вариант –опорные точки находятся в пространстве (объемная трех координатная обработка)»[7].На практике для перемещения инструмента системе ЧПУ недостаточно только опорных точек, необходимо более детальное ее представление. Для этого используется специальное вычислительное устройство –интерполятор. Он рассчитывает промежуточные точки и выдает соответствующие команды. Интерполяторы, как правило, подразделяются на линейные и круговые. Для отработки прямолинейного движения инструмента используется линейный интерполятор. Информация о координатах опорных точек поступает на вход. Для каждой координаты узловой точки вырабатывается последовательность импульсов, которые необходимы для отработки заданной геометрии. Эта информация приходит на выход. Но допустить точное соответствие перемещения вдоль заданной прямой бывает сложно. Итоговая траектория перемещения приближенно напоминает ломаную линию (рисунок 1).Рисунок 1 –Линейная интерполяция Интерполятор,  посылая  необходимое количество импульсов на привода, в процессе отработки прямой поочередно управляет включением приводов то по оси X, то по оси Y(если прямая лежит в плоскости XY). На рисунке 1 для отработки прямой на ось на ось X посылается два импульса, а на ось Y-один импульс. Значение d называется допустимой погрешностью и определяет отклонение от заданной геометрии. Таким образом, линейный интерполятор рассчитывает нужное количество импульсов по той или иной оси и выдает их на привода[8].

56 Евразийский Союз Ученых (ЕСУ) #7(76), 2020 Если движение инструмента осуществляется по дуге, то говорят о круговой интерполяции. Первые системы ЧПУ оснащались линейными интерполяторами, и программирование такого движения для программиста было затруднено. Дуги и окружности приходилось аппроксимировать (заменять) прямыми линиями, т.е. просчитывать промежуточные точки. На рисунке 2 необходимо линейно аппроксимировать участок дуги AB. Отклонение от округлости с радиусом R определяется расстоянием d, очевидно, что чем меньше величина линейного участка dl, тем выше точность аппроксимации. Зная допустимую погрешность аппроксимации d можно рассчитать угловой шаг df = arcos((R-d)/R), a число сегментов аппроксимации на заданном участке n = f2-f1/df [8]. Рисунок 2 –Круговая интерполяция Линейно-круговые интерполяторы позволяют отработать движение как по прямой, так и по дуге. Благодаря такому устройству можно избавиться от сложных рутинных вычислений. Теперь рассмотрим, как осуществляется процесс фрезерования. Обработка контура обеспечивается совокупным движением детали по осям X и Y, закрепленной на столе станка. Вертикальное перемещение инструмента по оси Z отсутствует. Обработка контура 1 производится фрезой 3, перемещаемой по траектории 4, эквидистантной к заданному контуру (рисунок 3). Эквидистантой принято называть линию, равноотстоящую от обрабатываемого контура детали на расстояние, равное радиусу режущего инструмента. Разделим траекторию фрезы на элементарные участки, в качестве которых используются прямая и окружность (дуга окружности). В данном примере таких участков будет шесть: 1─2; 2 ─ 3; 3 ─ 4; 4 ─ 5; 5 ─ 6; 6 ─ 1. Точки 1 –6 называются узловыми или опорными[3].

Евразийский Союз Ученых (ЕСУ) # 7(76), 202057 Рисунок 3 –Обработка контура на вертикально-фрезерном станке При расчете эквидистанты переход от координат х0, у0 основного контура к координатам хэ, уэ эквидистантного контура (рисунок 4) осуществляется по формулам [4]. 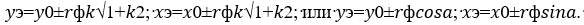 Где rф–радиус фрезы;  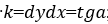α-угол наклона касательной в точке х0, у0. Если в алгоритмы интерполяции и алгоритмы управления приводами подач входят составляющие вектора контурной скорости, то они определяются: -для кругового контура  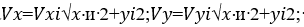-для линейного контура  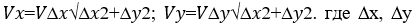кадровые перемещения по осям X, Y; V, Vх, Vу–соответственно контурная скорость подачи и ее составляющие; хи, уи–координаты центра дуги относительно ее начальной точки; хi, уi–координаты текущей точки дуги окружности относительно ее центра; Рисунок 4 –Переход от координат основного контура к координатам эквидистантного контура

58 Евразийский Союз Ученых (ЕСУ) #7(76), 2020 Разработаем управляющую программу. Выберем для исследования требуемый контур отработки движения (рисунок 5) [2]. Рисунок 5 –Обработка контура Применим все имеющиеся знания по линейной и круговой интерполяции и составим программу, используя G-код. Центр фрезы и траектория движения показаны на чертеже кругом со стрелкой, указывающей направление. Диаметр фрезы выберем равным 12. Сама деталь имеет форму цилиндра диаметром 60. Как должна проводиться обработка контура детали показано на рисунке 5. Теперь приступим непосредственно к написанию кода: N 5 G17 G54 G90N10 T1 M6N15 M3 S1000N20 M8N25 G1 G41 X-22.5 Y-30 F2500N30 Z-2N35 Y15 F 100N40 X-15N45 G3 X15 Y15 CR=15N50 G1 X22.5N55 Y-11.5N60 X19 Y-15N65 X-50N70 G40N75 G1 Z10 F2500N80 M9N85 M5N90 M2 Рассмотрим строку N25. Здесь мы применили команду G1(линейная интерполяция) и указали координаты (X,Y), к которым будет осуществляться подвод инструмента.

Дальнейшее движение будет происходить линейно до отмены этой команды. Также мы использовали команду G41, которая означает, что обработка контура будет осуществляться по эквидистанте [1].Теперь перейдем к строке N45. Здесь используется команда G3(движение по окружности против часовой стрелки). Помимо G3 мы также прописываем координаты конечной точки и указываем радиус окружности. Данная управляющая программа проверена и может использоваться для обработки рассматриваемого контура. Заключение.

Широкие возможности взаимодействия многих дисциплин и решение практических задач позволили нам в исследовании показать принцип решения геометрической задачи (определение координат, расчет перемещения, скорости).

Методы интерполяции позволяют создать необходимую геометрию движения рабочего инструмента, тем самым упростить процесс, и сделать качественную обработку.

В статье основное внимание уделено решению геометрической задачи движения инструмента по заданной траектории. Разработана программа и принцип, как можно провести обработку любой детали по сложной траектории по заданному алгоритму на станке с числовым программным управлением. Установили, что линейно-круговые интерполяторы позволяют отработать движение как по прямой, так и по дуге.