ПРОГНОЗИРОВАНИЕ ОЖИДАЕМОГО СПРОСА НА ЗИП

Прогнозирование ожидаемого спроса возможно, если известны количество отказов и нормы расхода в определенный период времени. Чем прогноз точнее, тем меньше будет на складе избыточного количества ЗИП.

Параметры, применяемые при прогнозировании:

- квалификация сотрудников;

- количество циклов эксплуатации оборудования;

- периодичность прохождения ТО;

При дальнейших исследованиях необходимо будет определить степень влияния каждого из параметров на работоспособное состояние используемого оборудования, коррелируемость параметров.

Выделим четыре параметра, которые влияют на потребность в ЗИП.

Первый параметр – стаж работы сотрудников. Качество выполняемых работ зависит от стажа работы сотрудника.

Второй параметр – количество циклов эксплуатации оборудования. Сколько раз система работала при полной сборке схем без отказов элементов и с отказами элемента.

Третий параметр – периодичность прохождения ТО.  Периодичность замены указанных деталей в инструкции эксплуатации значительно уменьшит отказы во время его работы.

Нередко на практике прогнозирование спроса осуществляют только на базе средних значений. Некоторые организации для упрощения расчетов нередко осуществляют краткосрочное прогнозирование на базе значений величин спроса, которые в лучшем случае являются средними и не учитывают элемента неопределенности. Прогнозирование выполняется в зависимости от потребностей, по методу экспоненциального выравнивания.

Такие прогнозы обычно бывают чрезмерно оптимистическими, не учитывают элемента неопределенности и приводят к значительным колебаниям величин запасов. Более реальным является такое прогнозирование, в котором наряду со средним значением (математическим ожиданием) определяется и оценивается возможная ошибка. В связи с этим решаются задачи улучшения прогнозов и стратегии управления запасами с учетом ошибок прогнозирования спроса.

В дальнейшем будем использовать среднесрочные прогнозы, т.к. охватывают период от 2 до 5 лет и зависит от периодичности использования ЗИП.

В практических расчетах для прогнозирования ЗИП, в том случае, если имеется информация о влияющих параметрах, часто используются регрессионные модели. Для учета влияния различных параметров на расход запасных частей и установление связей между самими параметрами необходимо построение многофакторной регрессионной модели.

Расход запасных частей в этом случае будет результативным признаком, а остальные переменные будут параметрами признаков x₁…x_m.

В общем случае уравнение регрессии для прогнозирования потребности в запасных частях выглядит следующим образом:

y=a₁x₁+a₂x₂+ a₃x₃                                                                     (1)

где переменные x_1…3 – являются параметрами признаков.

Чтобы построить многофакторную регрессионную модель результативного признака, необходимо вычислить коэффициенты парной корреляции (r_yx1,r_x2,r_x3):

                                                      (2) 

где  – среднеквадратичные ошибки соответствующих выборок.

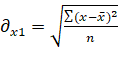;                                     (3)

Оценки параметров модели a₀,a₁,a_2,a₃ уравнения регрессии с помощью метода наименьших квадратов представим в матричном виде.

Уравнение регрессии с оцененным параметром:

=X ∙ a + e                                                           (4)

где:

Х – матрица значений независимых параметров;

e – вектор ошибок уравнении с оцененными параметрами (e_i);

а – вектор оценок параметров (a_j).

В уравнении регрессии матрицы коэффициентов при неизвестных параметрах имеет вид:

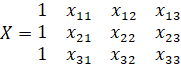
Вычисление параметров уравнения регрессии сложный и трудоемкий процесс. Существующие в настоящее время множество прикладных программ делают его автоматически.

После вычисления коэффициентов частичной корреляции, определяется коэффициент множественной корреляции r_y :

r_y = 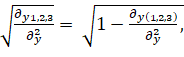                                      (5)

где:

∂_y1,2,3 – факторная дисперсия;

∂_y(1,2,3) – окончательная дисперсия;

 – результативная дисперсия.

         (6)

где:

 – расчетное значение результативного признака;

 - среднее значение результативного признака.

 – дисперсия , полученная с учетом параметров x₁, x₂, x₃;

 – дисперсия , полученная по элиминации влияния x₁, x₂, x₃.

Таким образом, коэффициент корреляции, как и величина дисперсии, характеризует качество подбора уравнения регрессии.

Система нормальных уравнений, параметры которых вычисляется по формулам:

  a_k = ;                                                     (7)

При анализе изменения расхода ЗИП значения n принимаются равными 12.

Спрос на ЗИП динамичен и подвергается колебаниям под влиянием множества технических, организационно-экономических и др. параметров. Период, в течении которого сохраняется спрос на запасные части и детали, зависит от их срока службы, условий эксплуатации и ремонта. Потребность в запасных частях и деталях носит неопределенный, вероятностный характер. Таким образом, запасные части и детали должны поставляться с некоторым опережением по отношению к возникающему спросу и должны постоянно находиться в запасах для своевременного устранения отказов. В связи с этим для ЗИП необходимо прогнозирование его спроса, которое может производиться на основе статистики их расходования.