ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ УСТАНОВКИ МЕТОДОМ СВОБОДНОГО ВЫБЕГА
Журнал: Научный журнал «Студенческий форум» выпуск №41(177)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №41(177)
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ УСТАНОВКИ МЕТОДОМ СВОБОДНОГО ВЫБЕГА
Современный электропривод представляет собой сложную многомассовую электромеханическую систему, динамические режимы работы которой описываются дифференциальным уравнением высокого порядка. Поэтому практически для решения задач динамики электропривода приходится принимать некоторые допущения. Так, если механические связи многозвенной системы электропривода можно принять абсолютно жесткими и все инерционные массы привести к оси вращения вала двигателя, а также если приведенный момент инерции системы Jпр постоянный, то механический переходный процесс одномассовой системы будет описываться одним дифференциальным уравнением движения для вращательного движения [1]
![]() , (1)
, (1)
устанавливающим связь между моментом ![]() , развиваемым электродвигателем на валу, моментом статической нагрузки
, развиваемым электродвигателем на валу, моментом статической нагрузки ![]() и моментом динамической нагрузки
и моментом динамической нагрузки
![]() . (2)
. (2)
Момент статической нагрузки в выражении (1) можно представить в виде суммы моментов – момента статического сопротивления рабочего органа ![]() механизма, обусловленного его полезной работой (например, работой грузоподъемного механизма крана), и момента трения
механизма, обусловленного его полезной работой (например, работой грузоподъемного механизма крана), и момента трения ![]() , обусловленного силами трения в кинематических звеньях механической части электропривода.
, обусловленного силами трения в кинематических звеньях механической части электропривода.
Динамический момент ![]() согласно (2) возникает под влиянием ускорений при изменениях скорости движения wд. Приведенный момент инерции системы электропривода определяется суммой, кг×м2:
согласно (2) возникает под влиянием ускорений при изменениях скорости движения wд. Приведенный момент инерции системы электропривода определяется суммой, кг×м2:
 ,
,
где ![]() – момент инерции ротора электродвигателя;
– момент инерции ротора электродвигателя; ![]() – момент инерции
– момент инерции
k-го элемента механической части, угловая скорость которого меньше в ![]() раз по сравнению со скоростью двигателя wд.
раз по сравнению со скоростью двигателя wд.
При исследовании, проектировании и эксплуатации электрических приводов инженеры сталкиваются с недостаточным количеством информации о той или иной установке. В частности, значение момента инерции может не указывается в технических каталогах на электрические двигатели. Проблема усугубляется еще тем, что вал двигателя соединяется с исполнительным механизмом через муфты, передаточные устройства и др., моменты инерции которых не известны. Поэтому их приходится учитывать либо приближенно, либо определять экспериментально. Существует множество экспериментальных методов определения момента инерции – методы крутильных или маятниковых колебаний, метод падающего груза и др.
Задачей исследования настоящей статьи является экспериментальное определение момента инерции электромеханической установки, представленной на рисунке 1, методом свободного выбега [2]. Необходимость этого обусловлена исследованием переходных режимов работы установки с последующим синтезом регуляторов замкнутой системы электропривода.

Рисунок 1. Электромеханический агрегат
Установка представляет собой электромеханический агрегат, состоящий из двух двигателей, валы которых соединены муфтой. Слева расположен двигатель постоянного тока независимого возбуждения серии ПЛ-072 с номинальной мощностью ![]() 180 Вт, номинальная частота вращения двигателя 1500 об/мин, номинальные напряжения питания обмоток якоря и возбуждения 110 В, справа – двигатель асинхронный серии АИР 6384 220/380 В.
180 Вт, номинальная частота вращения двигателя 1500 об/мин, номинальные напряжения питания обмоток якоря и возбуждения 110 В, справа – двигатель асинхронный серии АИР 6384 220/380 В.
Сущность метода свободного выбега состоит в следующем. Исследуемая установка разгоняется до некоторой установившейся скорости ![]() в режиме холостого хода (ХХ). После этого электродвигатель отключают от сети, и наступает процесс самоторможения, т. е. торможения исключительно за счет внутренних сил трения (трения в подшипниках электродвигателя и сочленённых с ним вращающих частей о воздух, трения щеток о коллектор и др.). На преодоление этих сил трения затрачивается кинетическая энергия, запасённая во вращающихся частях агрегата:
в режиме холостого хода (ХХ). После этого электродвигатель отключают от сети, и наступает процесс самоторможения, т. е. торможения исключительно за счет внутренних сил трения (трения в подшипниках электродвигателя и сочленённых с ним вращающих частей о воздух, трения щеток о коллектор и др.). На преодоление этих сил трения затрачивается кинетическая энергия, запасённая во вращающихся частях агрегата:
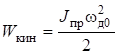 . (3)
. (3)
С другой стороны, эта энергия может быть определена как произведение мощности, затраченной на приведение во вращение агрегата в режиме ХХ ![]() (потери ХХ) на время работы
(потери ХХ) на время работы ![]() :
:
![]() . (4)
. (4)
Приравняв выражения (3) и (4), получим выражение для определения приведенного момента инерции исследуемой системы электропривода:
 . (5)
. (5)
Значения ![]() и
и ![]() , входящие в выражения (4) и (5), определяют экспериментально, выполнив опыт ХХ и опыт свободного выбега, предполагающий построение кривой выбега
, входящие в выражения (4) и (5), определяют экспериментально, выполнив опыт ХХ и опыт свободного выбега, предполагающий построение кривой выбега ![]() .
.
Опыт холостого хода [3] осуществляется подключением двигателя постоянного тока к сети с номинальным напряжением ![]() и разгона до установившейся скорости ХХ
и разгона до установившейся скорости ХХ ![]() . Мощность, затраченная на приведение во вращение агрегата в режиме холостого хода, Вт:
. Мощность, затраченная на приведение во вращение агрегата в режиме холостого хода, Вт:
![]()
где ![]() – номинальное напряжение, В;
– номинальное напряжение, В; ![]() – ток холостого хода, А;
– ток холостого хода, А; ![]() – сопротивление якорной цепи, Ом.
– сопротивление якорной цепи, Ом.
Для получения кривой выбега использовался программно-технический комплекс «Delta-Profi» [4] от научно-производственного предприятия «Учебная техника – Профи» (рисунок 2).

Рисунок 2. Переходный процесс скорости при свободном выбеге двигателя
Время ![]() определяется с помощью построения касательной к кривой выбега в точке начала торможения двигателя до ее пересечения с осью времени. Также, согласно рисунка 2, определяется частота вращения вала в режиме холостого хода
определяется с помощью построения касательной к кривой выбега в точке начала торможения двигателя до ее пересечения с осью времени. Также, согласно рисунка 2, определяется частота вращения вала в режиме холостого хода ![]() об/мин. Следовательно, угловая скорость холостого хода двигателя, рад/с:
об/мин. Следовательно, угловая скорость холостого хода двигателя, рад/с:
![]()
Тогда приведенный момент инерции исследуемого электромеханического агрегата согласно выражения (5) равен, кг/м2:

Следует иметь в виду, что большинство параметров трудно поддаются расчету и их приходится определять экспериментально. Кроме того, значения многих параметров, приводимых в каталогах, также устанавливаются в результате эксперимента, а их отклонение от фактических значений может достигать 10-20 % [5].

