Главная / Научный журнал «Студенческий форум» / №13(192) / Статья
Статья:

ИССЛЕДОВАНИЕ ВЗАИМОСВЯЗИ МАКСИМАЛЬНЫХ ПРОГИБОВ И СОБСТВЕННЫХ ЧАСТОТ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ МНОГОСЛОЙНЫХ КВАДРАТНЫХ ПЛАСТИН С ЖЕСТКИМ ОПИРАНИЕМ ПО КОНТУРУ

Журнал: Научный журнал «Студенческий форум» выпуск №13(192)

Рубрика: Технические науки

Выходные данные
Фокин Ф.В. ИССЛЕДОВАНИЕ ВЗАИМОСВЯЗИ МАКСИМАЛЬНЫХ ПРОГИБОВ И СОБСТВЕННЫХ ЧАСТОТ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ МНОГОСЛОЙНЫХ КВАДРАТНЫХ ПЛАСТИН С ЖЕСТКИМ ОПИРАНИЕМ ПО КОНТУРУ // Студенческий форум: электрон. научн. журн. 2022. № 13(192). URL: https://nauchforum.ru/journal/stud/192/108120 (дата обращения: 25.11.2024).
К условиям публикации Скачать журнал
Журнал опубликован
Мне нравится

Научный журнал «Студенческий форум» выпуск №13(192)

на печатьскачать .pdfподелиться

ИССЛЕДОВАНИЕ ВЗАИМОСВЯЗИ МАКСИМАЛЬНЫХ ПРОГИБОВ И СОБСТВЕННЫХ ЧАСТОТ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ МНОГОСЛОЙНЫХ КВАДРАТНЫХ ПЛАСТИН С ЖЕСТКИМ ОПИРАНИЕМ ПО КОНТУРУ

Фокин Фёдор Валерьевич
студент, Орловский государственный университет имени И. С, Тургенева, РФ, г. Орёл

 

Для оценки влияния жесткости связей сдвига на частоты собственных колебаний и прогибы двухслойной составной изотропной пластины со слоями различной цилиндрической жесткости рассмотрена квадратная в плане пластинка размерами a × b = 1000 × 1000 мм. Пластина была разбита на 400 конечных элементов (сетка разбивки 20×20). Конечные элементы пластин связаны как поперечными связями, препятствующие сближению и расхождению слоёв относительно друг друга, так и связями сдвига. Жесткость поперечных связей принималась постоянной ЕАпс = 83 кН. Жесткость связей сдвига ЕАсс для всех пластин изменялась в пределах от 10-6 до 106 кН.

Результаты расчета пластин с различными граничными условиями приведены в таблице 1. По данным таблицы 1 построен график изменения прогибов и частот колебаний в зависимости от жесткости связей сдвига ЕАсс..

Таблица 1.

 Результаты численных исследований

Защемлен ЖЖЖЖ

№ опирания

lgEAсс

круговая частота основного тона,             ω (с-1)

Максимальный прогиб, Wо мах (мм)

k=Wow2/(q/m)

отклонение k от kаналит %

1

2

3

4

5

6

1

-3

119,646

9,5

1,610

0,011

2

-2

119,656

9,5

1,610

0,027

3

-1

119,765

9,480

1,610

-0,001

4

0

120,824

9,290

1,606

-0,265

5

1

129,398

8,090

1,604

-0,384

6

2

156,952

5,490

1,601

-0,544

7

3

174,331

4,450

1,601

-0,543

8

4

177,406

4,280

1,595

-0,938

9

5

177,743

4,250

1,590

-1,258

10

6

177,776

4,220

1,579

-1,919

Защемлен ЖЖЖШ

№ опирания

lgEAсс

круговая частота основного тона,             ω (с-1)

Максимальный прогиб, Wо мах (мм)

k=Wow2/(q/m)

отклонение k от kаналит %

1

2

3

4

5

6

1

-3

75,99

21,8

1,490

-3,530

2

-2

76,006

21,8

1,491

-3,489

3

-1

76,453

21,700

1,502

-2,799

4

0

78,578

20,600

1,506

-2,525

5

1

93,48

14,700

1,521

-1,559

6

2

131,31

7,500

1,531

-0,899

7

3

167,654

4,640

1,544

-0,053

8

4

176,272

4,210

1,549

0,247

9

5

177,499

4,170

1,556

0,682

10

6

177,877

4,160

1,558

0,869

Защемлен ЖШЖШ

№ опирания

lgEAсс

круговая частота основного тона,             ω (с-1)

Максимальный прогиб, Wо мах (мм)

k=Wow2/(q/m)

отклонение k от kаналит %

1

2

3

4

5

6

1

-3

76,846

21,5

1,503

-3,514

2

-2

76,857

21,5

1,504

-3,486

3

-1

76,973

21,4

1,501

-3,645

4

0

79,599

20,4

1,530

-1,773

5

1

90,549

15,8

1,534

-1,552

6

2

124,78

8,44

1,556

-0,134

7

3

162,036

5,07

1,576

1,161

8

4

171,046

4,51

1,562

0,274

9

5

172,076

4,45

1,560

0,135

10

6

172,18

4,45

1,562

0,256

Защемлен ЖШШШ

№ опирания

lgEAсс

круговая частота основного тона,             ω (с-1)

Максимальный прогиб, Wо мах (мм)

k=Wow2/(q/m)

отклонение k от kаналит %

1

2

3

4

5

6

1

-3

76,287

22,79

1,570

0,342

2

-2

76,351

22,71

1,567

0,158

3

-1

76,452

22,64

1,567

0,113

4

0

78,182

21,55

1,560

-0,345

5

1

88,361

16,95

1,567

0,122

6

2

117,642

9,59

1,571

0,411

7

3

146,854

6,22

1,588

1,484

8

4

160,14

5,24

1,591

1,664

9

5

164,85

4,97

1,599

2,181

10

6

165,9853

4,94

1,611

2,968

Защемлен ШШШШ

№ опирания

lgEAсс

круговая частота основного тона,             ω (с-1)

Максимальный прогиб, Wо мах (мм)

k=Wow2/(q/m)

отклонение k от kаналит %

1

2

3

4

5

6

1

-3

67,541

28,15

1,520

-2,848

2

-2

67,845

28,13

1,533

-2,041

3

-1

68,211

28,010

1,543

-1,404

4

0

69,625

26,941

1,546

-1,194

5

1

78,624

21,320

1,560

-0,291

6

2

97,531

13,960

1,572

0,463

7

3

122,141

8,990

1,588

1,466

8

4

130,524

7,960

1,606

2,596

9

5

133,984

7,620

1,620

3,490

10

6

135,124

7,520

1,626

3,877

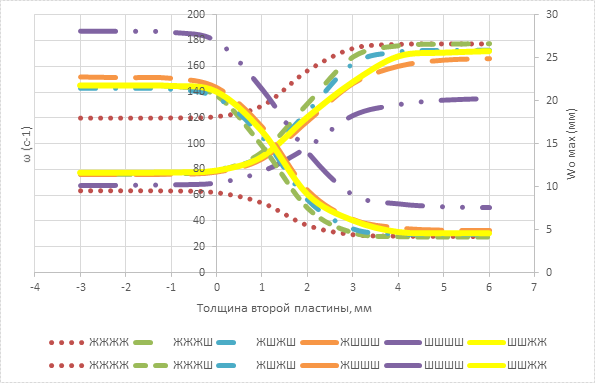
Рисунок 2.9. Взаимосвязь максимальных прогибов и частот собственных колебаний от изменения жесткости связей сдвига ЕАсс

 

Анализ полученных результатов показывает, что независимо от изменения жесткости связей сдвига ЕАсс фундаментальная зависимость (2.1) выполняется с точностью от -1,7764 до 3,877% для двухслойной пластины с комбинированными граничными.

 

Список литературы:
1. Коробко, В.И. Об одной "замечательной" закономерности в теории упругих пластинок [Текст]/В. И.Коробко.// Изв. вузов. Строительство и архитектура. –1989. –No 11. –С. 32-36.
2. Марфин Кирилл Васильевич. Взаимосвязь максимальных прогибов и собственных частот поперечных колебаний составных пластин на податливых связях: диссертация ... кандидата технических наук: 05.23.17 / Марфин Кирилл Васильевич;[Место защиты: Федеральное государственное бюджетное образовательное учреждение высшего образования «Юго-Западный государственный университет»].- Курск, 2015.- 145 с.
 

Похожие статьи

Больше статей