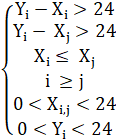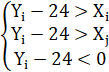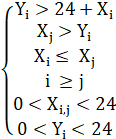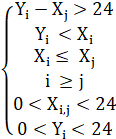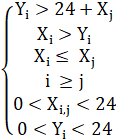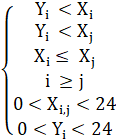ИССЛЕДОВАНИЕ МЕТОДОВ КОРРЕКЦИИ ЗАПИСЕЙ СИСТЕМЫ УЧЕТА РАБОЧЕГО ВРЕМЕНИ

Система учета рабочего времени — это аппаратно-программный комплекс, предназначенный для сбора и обработки данных о физическом входе и выходе сотрудников с территории предприятия. Данные, полученные этой системой, используются для расчета заработной платы в конце месяца.

Записи о входе и выходе в эту систему поступают путем ручного ввода сотрудником охраны. Такой способ введения порождает различные ошибки в системе, что в свою очередь приводит к невозможности автоматизированного анализа средствами данного аппаратно-программного комплекса. Чтобы рассмотреть возможные типы ошибок, необходимо записать условия системы в формальном виде,

множества, 

  упорядоченное множество пар вида 

Порядок в данном множестве задается условием 

Множество F назовем корректным, если соблюдаются следующие условия:

2)        

Для простоты записи будем писать следующее сокращение: если .

Зададим свойства пар – возможные варианты ошибок

1) Если для выполняется условие  , то такое . Эквивалент данного условия в реальном мире – «между записью входа и выхода прошло более 24 часов»

2) Если  для выполняется условие   , то такое . Эквивалент данного условия в реальном мире – «запись о входе произошла позже записи о выходе»

Рассмотрим комбинацию строк :

Данные условия можно интерпретировать так: нашлась комбинация строк, в которой записи выхода совпадают, а записи входа различны».

Может ли быть случай, когда обе строки находятся в ошибочном состоянии?

Введем следующие обозначения.

Пусть  ,  

Запись AaBa  означает, что элемент A множества F обладает свойством a,  а элемент B множества  F обладает свойством b.

Всего существует 4 комбинации с ошибками:

1) AaBa

2) AaBb

3) AbBa

4) AbBb

Рассмотрим каждый случай по отдельности и найдем ответ на вопрос: «Имеет ли система хотя бы одно решение или не имеет вовсе?»

Рассмотрим первую комбинацию AaBa. Запишем условия в системе неравенств.

Перенесем 24 в левую в первом, втором и шестом условиях

Рассмотрим вторую комбинацию AaBb. Запишем условия в системе неравенств.

Выразим  из первого условия и перепишем второе условие

Получаем, что система не имеет решения, следовательно комбинация ошибочных строк AaBb невозможна.

Рассмотрим третью комбинацию AbBa. Запишем условия в системе неравенств.

Перепишем второе условие и выразим  из первого неравенства

Из первых двух условий можно получить новое неравенство

Но это противоречит условию 3 исходной системы, значит система не имеет решений, следовательно комбинация ошибочных строк AbBa невозможна

Рассмотрим четвертую комбинацию строк AbBb. Запишем условия в системе неравенств.

Получим новое неравенство

Данное неравенство имеет хотя бы одно решение в рамках системы

Например, 

В данной статье были реализованы попытки формально описать систему учета рабочего времени сотрудника, а также были рассмотрены в формальном виде возможные ошибки, появившиеся в последствии ручного ввода. Выводы, которые были получены в результате статьи могут лечь в основу при разработке системы учета рабочего времени сотрудников предприятия с автоматизированной коррекцией данных.