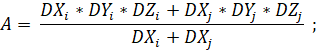УЧЕТ КРАЕВЫХ ЭФФЕКТОВ В ГИДРОДИНАМИЧЕСКИХ МОДЕЛЯХ СИСТЕМ РАЗРАБОТКИ НЕФТЯНЫХ И ГАЗОВЫХ МЕСТОРОЖДЕНИЙ
Журнал: Научный журнал «Студенческий форум» выпуск №20(243)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №20(243)
УЧЕТ КРАЕВЫХ ЭФФЕКТОВ В ГИДРОДИНАМИЧЕСКИХ МОДЕЛЯХ СИСТЕМ РАЗРАБОТКИ НЕФТЯНЫХ И ГАЗОВЫХ МЕСТОРОЖДЕНИЙ
ACCOUNTING FOR BOUNDARY EFFECTS IN HYDRODYNAMIC MODELS OF OIL AND GAS FIELD DEVELOPMENT SYSTEMS
Alfiya Iskhakova
Student, Ufa State Petroleum Technical University, Russia, Ufa
Iskandar Ibragimov
Student, Ufa State Petroleum Technical University, Russia, Ufa
Aivar Atlasov
Student, Ufa State Petroleum Technical University, Russia, Ufa
Аннотация. Данная статья посвящена исследованию подхода учета краевых эффектов в синтетических гидродинамических моделях. Рассмотрены подходы к решению задачи оценки прогнозных профилей добычи различных систем разработки. Выделены преимущества синтетических гидродинамических моделей. Рассмотрен подход замыкания противоположных граней модели через задание несоседних соединений.
Abstract. This article describes the study consideration of the boundary effects in synthetic hydrodynamic models. Approaches to solving the problem of estimating predictive production profiles of various development systems are considered. The advantages of synthetic hydrodynamic models are highlighted. The approach of closing the opposite faces of the model by specifying non-neighbor connections is considered.
Ключевые слова: гидродинамическое моделирование, учет краевых эффектов, несоседние соединения.
Keywords: hydrodynamic modeling, consideration of boundary effects, non-neighbor connections.
При проведении технико-экономического обоснования разработки месторождения возникает задача оценки прогнозных профилей добычи различных систем разработки. Данная задача, в зависимости от конечных целей и вычислительных ресурсов, может быть решена различными способами:
- использование аналитических моделей;
- построение полномасштабной геолого-гидродинамической модели месторождения или его участка;
- расчет показателей разработки на модели синтетического сектора [2,3].
Гидродинамические модели представляют собой систему уравнений сохранения массы и фильтрации, решаемую с применением численных методов, использующих конечно-разностные схемы для получения приближенного решения. Такой подход подразумевает решение системы алгебраических уравнений в конечном множестве точек за счет дискретизации по времени и по пространству.
Дискретизация по пространству задается путем определения расчетной сетки модели, которая воспроизводит геометрию моделируемого объекта. Для заданной сетки задаются различные свойства объекта, такие как пористость, проницаемость, начальная насыщенность пластовыми флюидами (доли объема пласта, занимаемые нефтью, газом и водой) и другие. Добывающие скважины в модели задаются в виде стоков, нагнетательные – в виде источников [1].
Стоит отметить, что проведение расчетов на полномасштабной модели позволяет получить частное решение для определенного участка месторождения. Полномасштабные гидродинамические модели являются детальным представлением моделируемой области, учитывающим как структурные особенности геологических тел, так и вариацию петрофизических, а также фактическое расположение пробуренных и проектных скважин. Число активных ячеек (узлов пространственной дискретизации) в таких моделях, как правило, велико и может достигать порядка миллиона. В связи с этим расчет моделей данного типа продолжителен по времени и может обладать высокой степенью неопределенности в виду того, параметры пласта наиболее точно определены только в околоскважинной зоне.
Расчет полномасштабной модели требователен к вычислительным ресурсам, из-за чего рассмотрение большого числа вариаций параметров модели может быть затруднительным. Также этот способ имеет ограничение по масштабируемости результатов. Результаты расчетов привязаны к определенному участку месторождения с учетом его локальных геологических особенностей и, в общем случае, не могут быть применены для оценки показателей добычи на других участках.
Чтобы выйти за пределы обозначенных ограничений полномасштабной модели, могут быть использованы модели синтетического сектора, составленные из геологических кубов с параметрами, характерными для той или иной площади месторождения и скважин, расставленных по регулярному шаблону. В этом случае становится возможным расчет профилей добычи различных систем разработки в фиксированных геологических условиях.
Под синтетическим сектором подразумевается секторная модель элемента разработки, границы которой ограничены размерами элемента разработки (рисунок 1). Элементом системы разработки называется элемент сетки скважины, описывающий в полной мере основную концепцию расстановки скважин на объекте. Так, к примеру, элементом разработки 9-точечной системы расстановки скважин (СРС) с организованной в ней системой поддержания пластового давления (ППД) будут являться 8 добывающих скважин, расположенных на равном расстоянии друг от друга, и 1 нагнетательная скважина в центре.
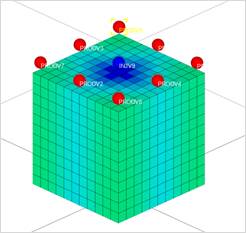
Рисунок 1. Единичный девятиточечный элемент разработки
Использование синтетических секторов позволяет оценить показатели работы «среднего элемента разработки» и может быть использовано при проектировании регулярных систем расстановки скважин. К тому же такие модели имеют относительно высокую скорость расчета, что позволяет проводить серии многовариантных расчетов для обоснования оптимального проектного решения.
При моделировании регулярных систем расстановки скважин, в частности с трещинами ГРП, контур гидродинамической модели не совпадает с контуром выбранного шаблона расстановки скважин - фактической границей моделируемой системы (так как трещины выходят за ее пределы), которая представляет собой границу элемента симметрии. Обычно она выделяется по границам зон дренирования, и, таким образом, должна являться линией непротекания [1].
Вследствие этого без дополнительных модификаций представление скважин на границе модели будет некорректным: скважины на краях модели, будут испытывать влияние только скважин внутри контура, то есть учет влияния соседних элементов на скважины отсутствует.

Рисунок 2. Проблематика краевых скважин в моделях регулярных СРС
Для исключения подобных краевых эффектов можно применить несколько подходов:
1. Задание множителей на поровый объем и проводимость краевых ячеек и задание множителей на продуктивность скважин.
В данном способе предполагаются задание дополнительных кубов свойств, модифицирующих поровый объем и проводимость ячеек вдоль осей, а также задание множителей на продуктивность скважин.
2. Замыкание противоположных граней модели через несоседние соединения.
В данной статье будет подробно рассмотрен второй способ.
Гидродинамическая модель представляет собой набор ячеек, распределенных в пространстве по заданной сетке. Между соседними ячейками осуществляется переток флюида, интенсивность которого определяется коэффициентом проводимости соединения.
Проводимости между ячейками рассчитываются по формуле:
|
|
(1) |
где
![]() – проводимость блока
– проводимость блока ![]() в направлении X;
в направлении X;
![]() – константа Дарси равная 0.00852702;
– константа Дарси равная 0.00852702;
![]() – коэффициент проводимости, в данном случае равняется 1;
– коэффициент проводимости, в данном случае равняется 1;
![]() – коррекция наклона, в данном случае равна 1;
– коррекция наклона, в данном случае равна 1;
![]() − площадь границы раздела между ячейками i и j:
− площадь границы раздела между ячейками i и j:
|
|
(2) |
![]() − коэффициент, для данного примера
− коэффициент, для данного примера ![]()
![]() – размеры ячеек в направлении X, Y, Z соответственно;
– размеры ячеек в направлении X, Y, Z соответственно;
![]() – проницаемость блока
– проницаемость блока ![]() .
.
В современных гидродинамических симуляторах существует опция задания дополнительных соединений между ячейками, не являющимися соседними (NNC - Non-Neighbour Connection). В виду этого, становится возможным учет краевых эффектов за счет задания перетока между противоположными гранями модели. Таким образом, моделируемый элемент симметрии полностью замыкается, а скважины, находящиеся на границах модели, испытывают взаимовлияние со скважинами на противоположной стороне контура (рисунок 3).
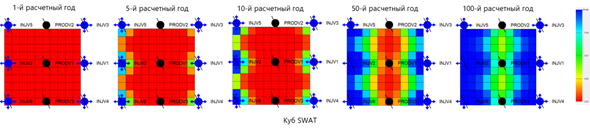
Рисунок 3. Пример динамики изменения водонасыщенности в модели с замыканием границ через NNC
В общем случае, корректное замыкание через NNC может быть достигнуто путем исключения одного вертикального и одного горизонтального ряда ячеек на границе модели и соединения через NNC полученных границ (рисунок 4). В случае, когда скважины в модели целиком располагаются в пределах ее контура, корректное замыкание через NNC может осуществляться исключением одного вертикального ряда ячеек на границе модели.
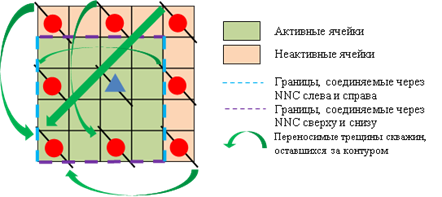
Рисунок 4. Представление элемента симметрии в модели с замыканием через NNC
Трещины ГРП в модели могут задаваться методом источников, в это случае радиус притока флюидов к скважине изменяется за счет добавления новых виртуальных перфораций. Таким образом, трещина моделируется как совокупность дополнительных перфораций (источников или стоков), расположенных по одному в каждом расчетном блоке сетки, через который она проходит.
Эту особенность необходимо учитывать при задании несоседних соедиений. Если в элементе присутствуют краевые скважины за границей активной области, с трещинами ГРП, затрагивающими активную зону модели с NNC, перфорации ГРП должны быть сохранены в модели путем их переноса на скважины находящиеся в активной области (рисунок 5).
Пример переноса перфораций трещин ГРП для девятиточечного элемента разработки показан на рисунке 5.

Рисунок 5. Пример переноса перфораций трещин ГРП
Было произведено сравнение результатов расчета показателей разработки рассчитаных на модели с замыканием модели через несоседние соединения и полученных путем выгрузки с центрального элемента (выделен желтым квадратом) в модели с 9 репликациями элемента разработки. (рисунок 6).

Рисунок 6. Модель девятиточечного элемента разработки с 9 репликациями
На рисунке 7 представлен график накопленной добычи жидкости, полученный различными методами, по нему видно, что расчеты совпадают.
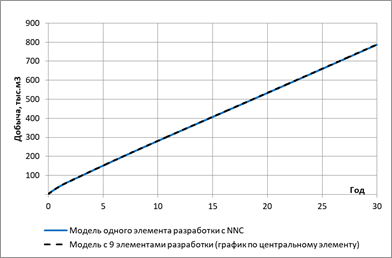
Рисунок 7. Сравнение расчета накопленной добычи жидкости в однородных моделях с различным учетом краевых эффектов
Таким образом, в случае однородного коллектора замыкание через NNC позволяет корректно воспроизвести модель элемента симметрии и учесть взаимовлияние скважин в сформированных регулярных системах разработки. Это позволяет воспроизвести динамику работы элемента разработки, как если бы он находился в бесконечном поле. При этом время расчета относительно модели с репликациями существенно сокращается, что достаточно важно при проведении многовариантных расчетов.
Выводы
Модель, ограниченная непроницаемыми границами, не в полной мере описывает модель синтетического сектора по причине искажения границ зоны дренирования. Поэтому необходимо вводить некоторые модификации для учета краевых эффектов в модели, такие как задание дополнительных множителей для краевых ячеек, или замыкание модели через несоседние соединения.
Влияние на элемент разработки соседних элементов в достаточной мере учитывается путем замыкания противоположных граней модели через несоседние соединения, однако необходим правильный учет трещин ГРП краевых скважин.