ПОСТРОЕНИЕ ДИНАМИЧЕСКОЙ СИСТЕМЫ 2-ГО ПОРЯДКА В MATLAB SIMULINK

Рассматривается дифференциальное уравнение

записанное относительно функции , функция  предполагается известной.[1-2]

Очевидно, что решение этого дифференциального уравнения тождественно совпадает с решением системы:

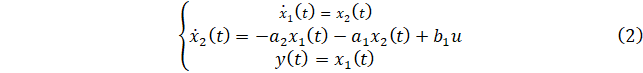
с начальными условиями .

Переходя в пространство изображений Лапласа, построим передаточную функцию

С её помощью можем записать:

С помощью вычислительного пакета Matlab проведу проверку сказанного. На рисунке 1 приведена схема, собранная в редакторе SIMULINK, позволяющая численно реализовать решение дифференциального уравнения , записанного в формах  и 

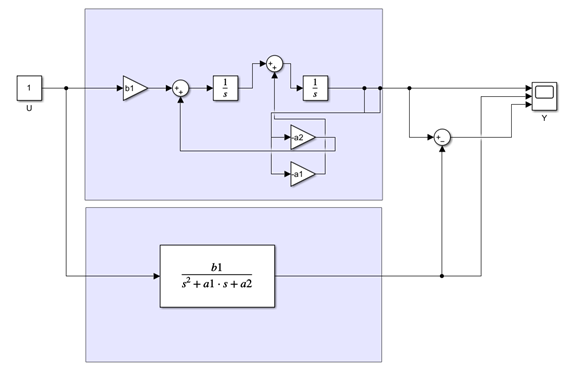
Рисунок 1. Схема Simulink

На рисунке 2 представлено решение, отвечающее системе , системе  и их разности.

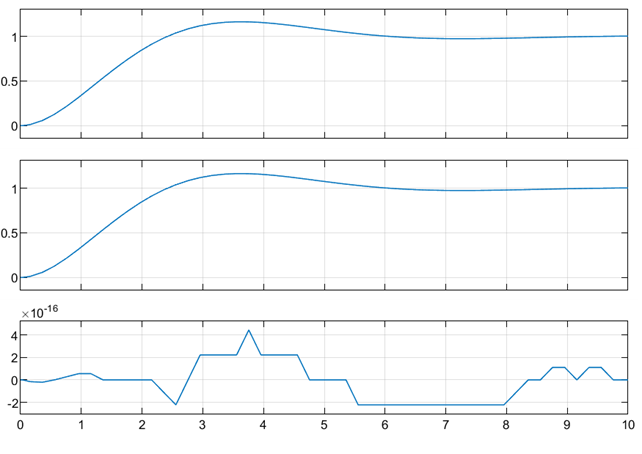
Рисунок 2. Результаты решения в SIMULINK

Как следует из рисунка 2, решения  и , как и ожидалось, тождественно совпадают.