ПОСТРОЕНИЕ СТОХАСТИЧЕСКОЙ МОДЕЛИ С ИСПОЛЬЗОВАНИЕМ МЕТОДА ПОДСТРАИВАЕМОЙ МОДЕЛИ

Ключевые слова: математическое моделирование, стохастическая модель, планирование факторного эксперимента, MS Excel «Поиск решения».

Математические модели – это мощный инструмент, используемый для абстрагирования и анализа сложных систем и процессов в реальном мире. Эти модели представляют собой математические аппроксимации реальных объектов, позволяя нам понимать и предсказывать их поведение. Математические модели описывают объекты и процессы с использованием различных математических выражений, таких как алгебраические уравнения, интегральные и дифференциальные уравнения, а также логические отношения. Однако следует помнить, что математическая модель всегда является идеализированным представлением реальности.

В зависимости от характера описания причинно-следственных связей и изменений во времени, можно выделить несколько типов моделей: детерминированные и стохастические.

Детерминистические модели характеризуются отсутствием случайных изменений. Все поведение объекта в таких моделях определяется конкретными начальными условиями и входными данными. Это означает, что в детерминистических моделях все аспекты поведения системы полностью определены.

Стохастическая модель учитывает случайные изменения в данных, что отличает ее от детерминированных моделей, и оценивает вероятность изменения значений переменных. Примером стохастической модели является модели стохастического процесса, часто использующиеся в моделировании каких-либо экономических процессов.

В статье речь пойдёт о построении стохастической модели [1]. Цель и предмет исследования были получены от руководителя – процесс усвоения кислорода в кислородном конверторе.

В процессе сбора информации об объекте стало теоретически известно, что коэффициент усвоения кислорода зависит от нескольких факторов: расхода кислорода, положения кислородной фурмы относительно зеркала металла и температуры расплава, при которой происходит продувка.

Задачей исследователя является осуществление экспериментов с данным объектом в соответствии с планом полного факторного эксперимента (ПФЭ), в котором факторы модели изменяются на двух уровнях: высоком (+1) и низком (-1). В рамках ПФЭ стремятся получить математическую модель, например, с использованием уравнения (1), где a – коэффициенты модели, x – входные параметры.

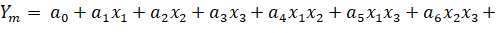
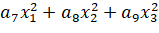                                           (1)

Для реализации опытов на выданном искусственном объекте необходимо:

1. Запустить программу «Model»
2. Из матрицы планирования выбрать вариант опыта, установить значения факторов, соответствующие этому опыту и запустить программу кнопкой «Пуск»
3. Выждать, пока не пройдет переходный период, связанный с инерционностью объекта
4. Через кнопку «Стоп» остановить программу и занести значение коэффициента усвоения кислорода в таблицу ПФЭ, как первое повторение опыта Y1
5. При тех же значениях входных параметров запустить программу на любое время, после чего вновь остановить и записать повторное значение коэффициента усвоения кислорода в графу Y2
6. Возвращаться к пункту 2 до заполнения всех 8 строк таблицы наблюдений, после чего произвести расчет построчных средних значений Yср.

На Рисунок 1и Рисунок 2соответственно показаны интерфейс программы модели-имитатора, с помощью которой осуществляется опыт, а также матрица планирования ПФЭ, заполненная значениями, полученными в результате опыта.

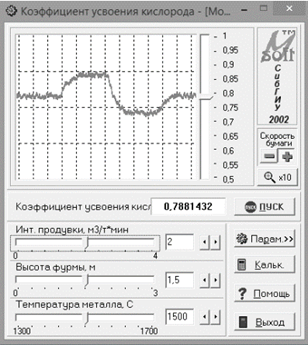
Рисунок 1. Интерфейс модели-имитатора

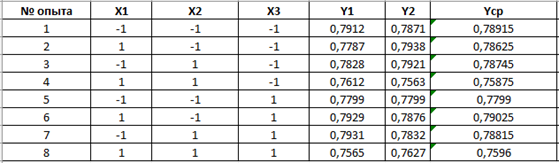
Рисунок 2. Заполненная матрица планирования ПФЭ

Четвертый этап фокусируется на параметрической идентификации объекта, что включает в себя настройку коэффициентов модели [2]. Эту настройку можно провести с использованием двух типов методов: без поиска и с поиском. К первой категории относятся различные модификации метода наименьших квадратов, а ко второй – методы подстраиваемой модели.

На Рисунок 3изображена схема подстраиваемой модели, использующей встроенный оптимизатор "Поиск решения" в MS Excel. Принцип работы метода заключается в следующем: для каждого опыта вычисляется квадрат разницы между фактическим значением выходного параметра и модельным значением при одинаковых входных параметрах. Затем, с использованием оптимизатора "Поиск решения", коэффициенты модели A0 - Am настраиваются таким образом, чтобы минимизировать сумму квадратов этих разностей по всем опытам.

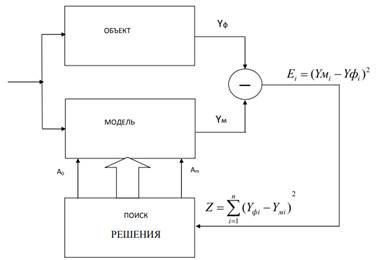
Рисунок 3. Схема подстраиваемой модели

Реализация метода подстраиваемой модели производится следующим образом:

1. На том же листе MS Excel, формируется таблица коэффициентов модели
2. Используя возможности MS Excel, рассчитать значения Yмодель для всех 16 опытов, для этого к таблице ПФЭ добавить справа ещё один столбец.
3. Аналогично, добавив ещё один столбец – Ем (ошибку модели), рассчитать построчные значения квадрата разности между фактическим значением выходного параметра Yср и модельным Yм.
4. Рассчитать сумму квадратов разностей по всем 8 опытам.
5. Открыть встроенную программу MS Excel - «Поиск решения»
6. Установить целевую ячейку. В текущей задаче это ячейка, в которой хранится сумма квадратов разностей
7. Необходимо оптимизировать ошибку модели до минимума
8. Изменять нужно ячейки переменных с коэффициентами модели
9. Запустить   программу «Поиск    решения»
10. После выполнения программы, в таблице коэффициентов будут установлены оптимальные значения этих коэффициентов, что представлено на Рисунок 4.

Рисунок 4. Подобранные значения коэффициентов модели

Следующим шагом, как правило, проводится статистическая проверка полученной модели на её адекватность. Выполнить данный этап можно при помощи расчёта и сравнения критерия Кохрена, определения значимости коэффициентов модели, а затем – непосредственно проверки адекватности модели, рассчитав и сравнив критерий Фишера относительно полученной модели. Однако в рамках полученной задачи данный этап не является обязательным к выполнению.

Таким образом, в ходе выполнения работы была выбрана комбинация моделей (линейная модель, нелинейная с взаимодействиями факторов, нелинейная со степенными зависимостями), описывающая исследуемый процесс, заполнена матрица ПФЭ и при использовании встроенного в MS Excel инструмента «Поиск решения» - подобраны оптимальные значения коэффициентов получившейся модели.