ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЗАВИСИМОСТИ ТЕМПЕРАТУРЫ РЕЗИСТОРА ОТ ВРЕМЕНИ ПРИ ВОЗДЕЙСТВИИ ПОСТОЯННОГО НАПРЯЖЕНИЯ И ЛИНЕЙНОГО ТЕМПЕРАТУРНОГО ИЗМЕНЕНИЯ СОПРОТИВЛЕНИЯ

CONSTRUCTION OF A MATHEMATICAL MODEL OF THE DEPENDENCE OF THE RESISTOR TEMPERATURE ON TIME UNDER THE INFLUENCE OF CONSTANT VOLTAGE AND LINEAR TEMPERATURE CHANGE OF RESISTANCE

Denis Bogdanov

Student, Bauman Moscow State Technical University, Russia, Moscow

Аннотация. В статье рассматривается построение математической модели зависимости температуры резистора от времени при воздействии постоянного напряжения и линейном изменении сопротивления. Автор принимает во внимание линейное изменение электрического сопротивления резистора в зависимости от температуры и выводит соответствующие формулы для расчета силы тока. Затем автор решает дифференциальное уравнение, описывающее изменение температуры резистора со временем, и получает функцию, связывающую температуру и время. Также обсуждается возможность использования обратной функции для определения температуры в любой момент времени. Статья включает выводы о влиянии различных параметров на процесс нагрева резистора.

Abstract. The article presents a mathematical model for the temperature-time relationship of a resistor subjected to a constant voltage with linear resistance variation. It takes into account the linear relationship between the electrical resistance and temperature of the resistor and derives relevant equations for calculating current strength. The paper then solves a differential equation to describe the temperature change over time and obtains an analytical function relating temperature to time. The feasibility of using this function to predict temperature at a specific time is also explored. Finally, the paper discusses the impact of various parameters on the thermal behavior of the resistor, drawing conclusions from the model.

Ключевые слова: математическая модель; температура; время; резистор; температурный коэффициент электрического сопротивления.

Keywords: mathematical model; temperature; time; resistor; temperature coefficient of electrical resistance.

В реальном мире при подаче постоянного напряжения в цепь резистор нагревается и может изменять свое сопротивление.

 Это может привести к изменению общего сопротивления цепи, а следовательно, и силы тока цепи, что в некоторых случаях может привести к неприятным ситуациям. Например, к расплавлению резистора.

Чтобы этого избежать, нужно построить математическую модель зависимости температуры резистора от времени.

Для начала примем то утверждение, что изменение электрического сопротивления R(T) происходит линейно, то есть процесс можно описать следующей формулой:

где R₀ – электрическое сопротивление при температуре T₀, Ом;

α – температурный коэффициент электрического сопротивления [6];

Т – температура, К;

T₀ – начальная температура, K.

Пусть наша цепь будет состоять из источника постоянного напряжения и данного резистора.

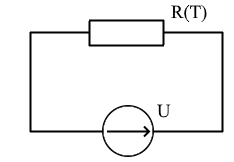
Рисунок 1. Электрическая цепь

Тогда сила тока может быть выражена следующей формулой:

где U – постоянное напряжение, В.

Так как возникла сила тока в цепи, то можно применить мощность резистора P, которая выражается следующим тождеством:

Известно, что мощность по определению является первой производной энергии по времени.

На резисторе не происходит внешнее воздействие, поэтому работа внешней силы равна нулю. Тогда, подставив в формулу (3) зависимость силы тока от температуры I(T) из выражения (2), и применив определение количества теплоты с удельной теплоемкостью, получим дифференциальное уравнение:

где C_m – удельная теплоемкость по массе, Дж/(кг*К);

m – масса резистора, кг;

dT – бесконечно-малое изменение температуры, К;

dt - бесконечно-малое изменение времени, с.

Решив данное уравнение, мы получим функцию t(T):

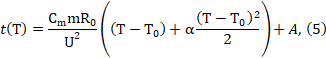
где A – некая постоянная при интегрировании, с.

В принципе с этой математической моделью можно работать. Например, вычислить через какое время резистор перейдет в стадию плавления или осуществить графическое построение зависимости температуры от времени. Однако в некоторых случаях может потребоваться воспользоваться её обратной функцией T(t). Так как полученная функция является квадратным трехчленом, то сначала нужно преобразовать её в следующий вид:

где B, t₀, D – некоторые постоянные.

Затем перенести все коэффициенты в правую сторону и взять квадратный корень. Так мы получим функцию, обратную квадратному трехчлену.

Сделав так, с нашей функцией (5) мы можем получить выражение T(t):

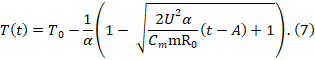
Из полученной формулы мы можем сделать несколько выводов:

- Если R₀, или m, или C_m будут намного превосходить напряжение U, то температура будет равняться T₀, то есть резистор никак не разогреется, что осложняет вычисление температурного коэффициента электрического сопротивления. Поэтому нужно подобрать такие значения R₀, m и Cm, чтобы напряжение U могло их превосходить.

- Если подать большое напряжение U, то температура будет быстро расти, что приведет к неприятной ситуации - плавлению резистора.

- Если температурный коэффициент электрического сопротивления α будет намного превосходить напряжение U, сопротивление R₀, массу и удельную теплоёмкость C_m, то данный резистор очень хорошо подойдет к производству электронных схем.

Таким образом с помощью данных математической моделей (5) и (7) можно рассчитать температурный коэффициент электрического сопротивления α для каждого материала и выбрать тот, что обладает наибольшим значением.