Модифицированный муравьиный алгоритм формирования производственного расписания вагонного депо

Введение

Все организационные и технологические решения в распределении работ на предприятиях должны приниматься оперативно. Причём неоптимальные решения значительно снижают эффективность построения расписаний работы производственного участка. Абсолютно такая же ситуация наблюдается и в депо по ремонту вагонов. Особенно актуальной задачей является построение оптимальных расписаний работы для работников вагонного депо в соответствии с технологическим маршрутом.

Разрабатываемый алгоритм должен эффективно распределять трудовые ресурсы ремонтного депо и увеличить его производительность. Задача распределения необходимых работ по ремонту вагонов среди работников относится к задачам оперативно-календарного планирования.

Анализ современных работ по комбинаторной оптимизации на графах (особенно динамических задач) показывает, что одним из самых перспективных подходов является использование муравьиных алгоритмов. Этот подход позволяет существенно улучшить систему оперативного планирования, тем самым, сократив время построения оптимальных или приемлемых производственных расписаний.

Математическая модель

Для оперативного планирования распределения работ технологический процесс разделяется на технологические операции. Допустим, что на данном производственном участке ремонтируется n вагонов d_i (i = 1, 2, …, n). Обозначим некоторую произвольную операцию, которую необходимо выполнить над вагоном d_i, через O_ij (j =1, 2, …, m_i), где m_i – общее количество операций, которые необходимо выполнить для ремонта вагона d_i. Под технологическим маршрутом работника обычно понимают порядок выполнения им работы над вагоном или же последовательность выполняемых операций:

М_i = ( О_i1,O_i2, … , О_imi )                                                                                                (1)

При этом необходимо учитывать следующие ограничения:

1. Ограничения по срокам изготовления:

T_пл > T_ф,                                                                                                       (2)

где: T_ф – фактический срок ремонта вагона d_i,

T_пл – плановый срок ремонта вагона d_i.

2. Ограничения по объемам изготовления:

N_пл = N_ф,                                                                                                   (3)

где:  N_ф – фактическое отремонтированное количество вагонов,

N_пл – заданное в производственной программе количество вагонов.

Задача оперативного планирования расписания работ заключается в том, чтобы для производственного участка с заданными технологическими маршрутами ремонта вагонов составить некоторое расписание, удовлетворяющее сформулированным условиям, которое представляется в виде последовательности чисел t_ij – моментов начала выполнения технологических операций O_ij.

Представим расписание работ в виде графовой модели.

Представление графа и муравья

По аналогии с графом, предложенным в статье «Графоаналитическая модель загрузки гибких производственных модулей автоматизированного технологического участка машиностроительного предприятия», было решено, что в роли вершины графа (Oij) будут выступать работы по ремонту, которые нужно выполнить рабочему над заданными вагонами, муравьями (Mij) будут выступать сами рабочие, а ребра графа – это переход от одной технической операции к другой.

Исходный узел графа определяет начало выполнения плана (стартовую точку), в которую помещаются муравьи, количество которых равно числу рабочих на производственном участке. Остальные вершины графа соответствуют отдельной технологической операции O_ij (согласно технологической карте). Каждый узел O_ij однозначно определяется параметрами:

O_ij = (K_min, K_opt, Тv_ij, Tn_ij, N_ij, Pr_ij, D, Kv, PI,NI),                                                                           (4)

где: K_min – минимальное количество рабочих, необходимых для выполнения технологической операции O_ij;

11. – оптимальное количество рабочих, необходимых для выполнения технологической операции O_ij;

Tv_ij – время выполнения технологической операции O_ij;

Tn_ij – время подготовки рабочего для выполнения технологической операции O_ij;

N_ij – номер рабочего, выполняющего работу O_ij;

• – приоритет технологической операции O_ij (в диапазоне от 1 до 10);
• – доступность технологической операции O_ij;
• – квалификация рабочего, необходимая для выполнения технологической операции O_ij;
• – список узлов графа, которые ведут в данный узел
• – список узлов графа, в которые можно перейти из данного узла

При этом муравьи имеют ограниченную популяцию и обладают рядом характеристик:

M_ij = (Kv, T, W, Ts, Tf),                                                                                               (5)

где: Kv – квалификация муравья (рабочего);

20. – количество времени, которое муравей (рабочий) затратит на выполнение всех работ в рамках одной смены;
23. – список работ, которые муравью (рабочему) нужно выполнить за смену;
24. – список времени, который содержит фактическое начало выполнения каждой работы из списка W в рамках рабочей смены;
25. – список времени, который содержит фактическое завершения каждой работы из списка W в рамках рабочей смены;

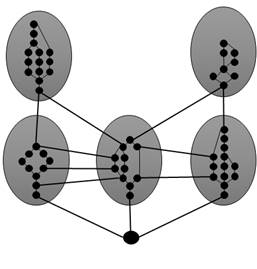
Рисунок 1. Графовое представление работ в вагонном депо

Этапы прохождения муравья по графам

Разработанный модифицированный муравьиный алгоритм для формирования производственного расписания вагонного депо можно представить в виде блок-схемы (Рис.2) со следующей последовательностью действий:

1) Формирование графа. В самом начале алгоритма формируется граф, на основании тех данных, которые ввел пользователь: необходимых работах по ремонту, которые нужно провести над вагонами, количество работ, которые нужно провести над вагонами. Это статичные данные, которые хранятся в базе данных программы.

2) Формирование популяции муравьев. Аналогичным образом формируется и популяция муравьев. Перед выполнением алгоритма имеется информация о рабочих, которые будут проводить ремонтные работы над вагонами, и она тоже статическая и хранится в БД программы.

3) Инициализация регулирующих параметров. Установка различных параметров, которые вводит пользователь перед запуском алгоритма, например приоритет выполнения технологических операций Pr_ij. Начальный расчет вероятностей перехода муравьев из стартовой точки в вершины происходит по следующей формуле:

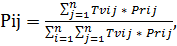
где:  P_ij – вероятность перехода на вершину графа;

Tv_ij – время выполнения технологической операции O_ij;

Pr_ij – приоритет выполнения технологической операции O_ij;

4) Всем муравьям, которые будут участвовать в прохождении графа, задается начальная (стартовая) точка.

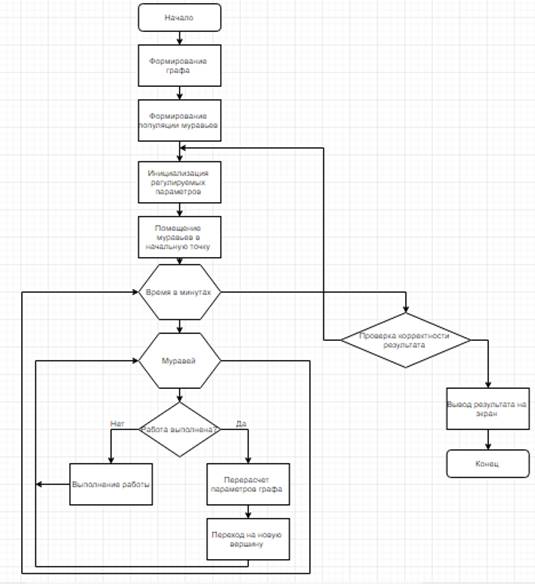
Рисунок. 2 Общий алгоритм

5) Начало выполнения непосредственно самого алгоритма. Его выполнение накладывается на временную шкалу, таким образом, что одна итерация алгоритма равна 1 минуте рабочего времени, то есть, если работа, которую выбрал муравей будет длиться 20 минут, то 20 итераций он будет бездействовать, а на 21-й выберет себе новую вершину и снова будет бездействовать определенное количество времени, равное времени выполнения выбранной им работы. Вероятность, по которой определяется, куда пойдет муравей будет рассчитываться двумя формулами, в зависимости от ситуации: 1) работа может выполняться одним муравьем, формула для расчета вероятностей будет выглядеть следующим образом:

где:  P_ij – вероятность перехода на вершину графа;

Tv_ij – время выполнения технологической операции O_ij;

Pr_ij – приоритет выполнения технологической операции O_ij;

2) на вершине графа находятся муравьи, но они не могут начать работу, так как их количества недостаточно. Эта работа будет в наивысшем приоритете у других муравьев и вероятность перехода на такую работу будет вычисляться по следующей формуле:

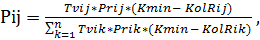
где:  P_ij – вероятность перехода на вершину графа;

Tv_ij – время выполнения технологической операции O_ij;

Pr_ij – приоритет выполнения технологической операции O_ij;

K_min – минимальное количество муравьев, которые должны участвовать в технологической операции;

KolR_ik - количество муравьев, которые уже участвуют в технологической операции

6) Каждую итерацию алгоритма муравьи будут опрашиваться на то, выполнена работа или нет. Если работа не выполнена, то муравей игнорирует все инструкции и продолжает её выполнять, если же он выполнил необходимую работу к этому времени, то он анализирует текущее состояние графа, которое изменилось во время его бездействия, пересчитывает свои параметры и снова выбирает для себя новую работу. Стоит отметить, что при каждом действии каждого муравья меняется общее состояние графа.

7) Выходными данными работы алгоритма является список графов, по которым прошел каждый муравей, у каждого он будет свой. После этого выполняется подсчет времени работ для каждого муравья и, если это время больше, чем плановое время выполнения работ по ремонту приоритетного вагона, то считается, что алгоритм отработал некорректно и осуществляется его перезапуск, но уже с новыми, отредактированными параметрами. Например, увеличение приоритета тех операций, которые были в списке того муравья, который не прошел проверку.

8) Если же алгоритм отработал корректно, результаты его работы выводятся пользователю на экран.

Выводы

В рамках данной статьи была описана общая структура модифицированного муравьиного алгоритма для распределения работ по ремонту вагонов в вагонном депо. Рассмотрены и описаны шаги данного алгоритма.

В результате была сформирована теоретическая база для реализации модифицированного муравьиного алгоритма. Целесообразно проводить исследования по оптимизации и улучшению разрабатываемого алгоритма.