ИЕРАРХИЧЕСКОЕ ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ В СИСТЕМЕ MATLAB + SIMULINK

Одним из ключевых преимуществ пакета расширения системы MATLAB+Simulink [1, 2] является возможность компонентного моделирования, позволяющего реализовать принципы модульного проектирования сложных цифровых устройств. Данный подход обеспечивает декомпозицию системы на функциональные блоки (подсистемы), которые могут разрабатываться и тестироваться независимо друг от друга. Также предоставляется возможность повторного использования компонентов и параллельной работы над проектом. Готовые компоненты можно сохранять как блоки в библиотеке или в отдельных файлах, что позволяет команде работать над ними параллельно.

Подсистема – это набор блоков, сгруппированных в один блок Subsystem [3]. Эти блоки обладают гораздо более широкой функциональностью, чем просто создание пользовательских элементов. Подсистемы служат инструментом для организации и структурирования графического интерфейса модели. Логически связанные блоки диаграммы можно объединять в подсистемы, которые затем отображаются в виде единых компонентов, значительно упрощая визуальное восприятие сложных моделей.

Для наглядного представления принципа модульного проектирования в системе MATLAB + Simulink была создана блочно имитационная модель одноразрядного сумматора, на базе которого показана идея наращивания числа разрядов и моделирование соответственно четырех-, восьми- и более разрядных суммирующих устройств.

Двоичный одноразрядный сумматор (SM) и его условное графическое обозначение (УГО) представлены на рис. 1.  Он имеет три входа и два выхода.  На входы А и В подаются двоичные числа – разряды первого и второго слагаемого, а на выходах S и Р формируются соответственно значения суммы и переноса в следующий (более старший) разряд. Этот разряд подается на вход С следующей секции суммирования в многоразрядном сумматоре.

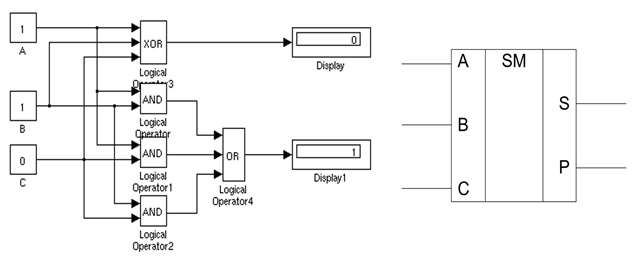
Рисунок 1. а) одноразрядный сумматор в системе Simulink и b) УГО SM

Очевидно, что получения двоичного четырехразрядного сумматора достаточно иметь четыре одноразрядных сумматора. Таблица истинности работы такого четырехразрядного сумматора, например, для чисел 7 и 11 представлена в таблице.

Таблица 1.

Таблица истинности четырехразрядного сумматора

Для повышения наглядности и удобства работы с цифровыми схемами достаточно инкапсулировать логику одноразрядного сумматора в отдельную подсистему (Subsystem). Тогда модель четырехразрядного сумматора может быть представлена последовательным соединением четырёх блоков одноразрядных сумматоров. Ход моделирования с результатом представления устройства – многоразрядный сумматор с использованием подсистем представлен на рис. 2.

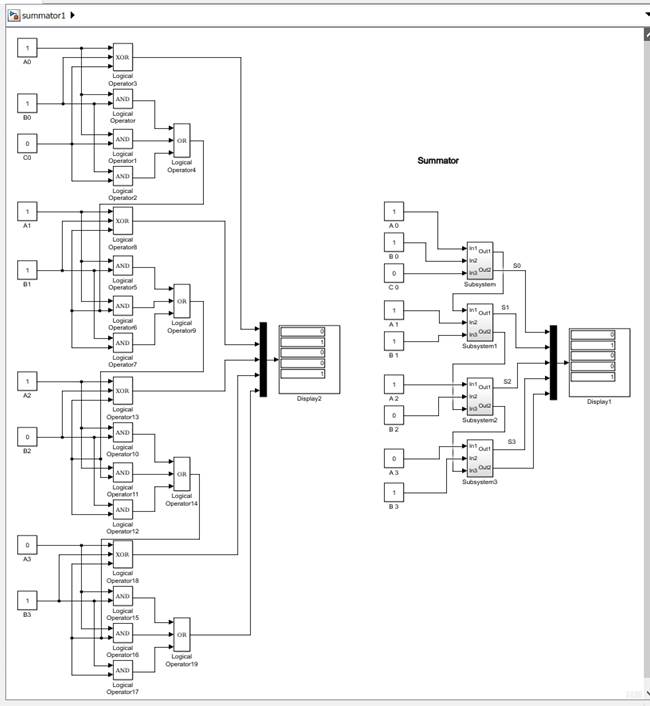
Рисунок 2. Модель четырехразрядного сумматора с использованием подсистем

В модели во входные блоки Const записываются разряды двоичных чисел A и B, причём младший разряд располагается в верхней части схемы, а старший – в нижней. Суммирование происходит с младших разрядов в сторону старших сверху вниз, путем формирования поразрядной суммы S и выходного переноса P, который в следующую секцию суммирования уже поступает как входной перенос С.

Используя описанный принцип, можно объединить уже четыре одноразрядные системы в подсистему большей степени интеграции и таким образом наращивать разрядность сумматора по правилу 2ⁿ (одно-, двух-, четырех и более числа разрядов).

Реализация сумматора с использованием подсистемы Subsystem в математической системе MATLAB + Simulink показала эффективную работу с блоками при блочно имитационном моделировании устройств и упростила структуру формирования сложной модели многоразрядного сумматора.

Описанные принципы и используемые методы могут помочь разработчикам повысить производительность моделируемых устройств за счет оптимизации вычислительных процессов, а также улучшить сопровождаемость программы и повысить эффективность командной разработки устройств и систем.