Использование компьютерной среды GeoGebra при подготовке к ЕГЭ по теме тригонометрия

Аннотация. В статье рассматриваются методические аспекты использования анимационных возможностей компьютерной системы GeoGebra в процессе обучения подготовки учащихся к ЕГЭ на основании заданий, связанных с тригонометрией. Представлен опыт использования анимационных возможностей компьютерной системы GeoGebra в процессе решения тригонометрических уравнений.

Ключевые слова: Компьютерная система GeoGebra, анимационные возможности, обучение тригонометрии, подготовка к экзамену, тригонометрические уравнения.

Одним из основных и обязательных разделов школьного курса математики является тригонометрия. Трудности, которые испытывают учащиеся в изучении тригонометрии, непосредственно связаны как с высоким уровнем абстракции понятий, так и с использованием числовой окружности как модели с помощью которой переопределяются тригонометрические функции и решаются многие задачи тригонометрии. Эти трудности в основном состоят в том, что нужно многое учитывать: определение тригонометрических функций и их свойства; направление вращения начального радиуса; значения тригонометрических функций и др. Особенно трудным для изучения является раздел тригонометрии, посвящённый обратным тригонометрическим функциям.

У большей части выпускников школ каждый год обнаруживается слабая подготовка по данному разделу математика, об этом свидетельствуют результаты единого государственного экзамена. Анализ работ показывает, что данный раздел является самым проблематичным, именно в этом разделе ученики допускают много ошибок, либо не приступают к таким заданиям. И базовый и профильный экзамен по математике содержит задания по данной теме.

Использование визуальных форм, несущих определенную смысловую нагрузку и делающих знание видимым, особо актуально при изучении основ тригонометрии.

Сопровождение занятий по подготовке к экзамену по математике компьютерными имитационными моделями и интерактивными иллюстрациями (анимационные чертежи, «живые» рисунки) значительно облегчает проникновение в сущность математических понятий и заданий.

Анимационные чертежи можно использовать на разных стадиях урока: как готовые наглядные пособия для повторения материала, как источник задач и сопровождения их решений, как инструмент для экспериментирования и проведения научных исследований, так и для закрепления и отработки заданий. Попутно ученик учится использованию компьютерных технологий не только в обучении, но и при решении исследовательских задач [Ларин, 2015].

Анимационное компьютерное моделирование математических объектов предполагает использование специализированных программ для создания компьютерной анимации: непрерывное вычерчивание графиков функций, вычерчивание различных кривых, моделирование разного рода преобразований и другое.

Возможность наглядного представления учебной информации посредством конструирования анимационных компьютерных моделей математических объектов и проведения, на их основе, компьютерных экспериментов и исследований, предоставляет компьютерная среда GeoGebra.

В данной статье представим опыт использования анимационных чертежей, созданных в компьютерной среде GeoGebra, в процессе подготовки к заданию на решение тригонометрических уравнений, которые встречается, как в профильном экзамене по математике, так и в базовом.

С методической точки зрения, посредством конструирования анимационных компьютерных моделей в среде GeoGebra, целесообразно обучающихся заранее на уроках познакомить с возможностями данной программы и ее основными функциями.

В качестве примера рассмотрим несколько заданий из базового ЕГЭ по математики.

Задание №5 Найдите корни уравнения:  

Задание направлено на решение тригонометрических уравнений. С помощью GeoGebrа мы создаем анимационный рисунок (рис 1.), который показывает модель решения подобных уравнений. Главная задача данного рисунка, заключается в том, чтобы наглядно показать обучающимся процесс нахождения корня.

Рисунок 1. Инструмент для вычисления тригонометрического уравнения cos x=a

Решение более сложных тригонометрических уравнений сводится к решению простейших тригонометрических уравнений.

Рассмотрим одно из заданий: Решите уравнение 2cosx+sinx=0 .

Для данного решения используется уже готовые тригонометрические функции. Главная задача анимационного рисунка, показать построения графиков, наглядность решения и алгоритм нахождения корня. Учащиеся должны понимать, какой способ применить для решения того или иного задания.

Чтобы решить данное уравнение нужно найти точку пересечения двух графиков. Первый график y=2cosx и второй график y’=-sinx.

Получаем следующее уравнение 2cosx= -sinx.

Построение(Рис.2):

1. Строим график y=2cosx
2. Строим график y’=-sinx
3. Отмечаем точку пересечения построенных графиков В.
4. Из точки В опускаем перпендикуляр на ось ОХ.
5. Абсцисса точки Е и есть искомый корень уравнения.

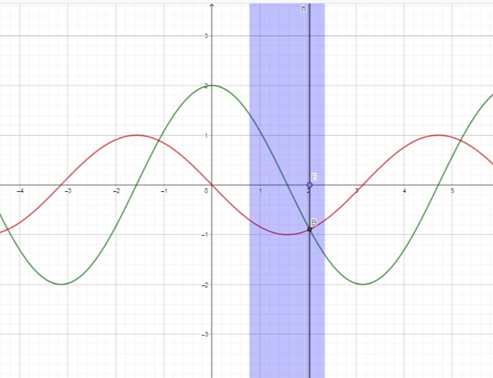
Рисунок 2. Инструмент для вычисления тригонометрического уравнения 2cosx+sinx=0

Анимационные модели должны быть помощниками для решения задач и для наглядного представления происходящих процессов при решении, а не выполнять все действия за учащихся.