Влияние процесса осадкообразования на фильтрацию жидкости из суспензии

Influence of sediment formation process on the liquid filtration from suspension

Tulegen Amanbaev

doctor of physical and mathematical sciences, Professor, Institute of mathematics and mathematical modeling, Almaty, Kazakhstan

Sholpanay Onalbaeva

Undergraduate, South Kazakh State University, Shymkent, Kazakhstan

Аннотация. Исследовано влияние седиментации дисперсной фазы и осадкообразования на процесс фильтрации жидкости из суспензии. Для описания поведения суспензии вне осадка используется система уравнений двухфазной смеси, а для описания движения жидкости через пористый слой осадка применяется уравнение фильтрации, основанное на законе Дарси. Анализируются формулы для движения межфазных поверхностей и характерных времен седиментации дисперсной фазы и фильтрации жидкости.  

Abstract. The influence of the dispersed phase sedimentation and precipitation formation on the liquid filtration process from suspension is investigated. To describe the dynamics of a suspension uses a system of two-phase mixture equations, and for the description of fluid motion through the porous layer of sediment is applied the filtering equation based on Darcy's law. Formulas for laws of motions of interfacial surfaces, characteristic times of sedimentation and filtration are analyzed.

Ключевые слова: суспензия; седиментация; фильтрация.

Keywords: suspension; sedimentation; filtration.   

Во многих практических задачах требуется изучить фильтрацию жидкости из суспензии через пористый осадок [1–3]. Целью данной работы является изучение взаимного влияния процессов фильтрации жидкости, седиментации частиц и осадкообразования.

Под действием силы тяжести частицы в суспензии осаждаются.  При этом происходит разделение фаз дисперсной смеси: на верхней части сосуда накапливается чистая жидкость, а внизу – осадок, высота которого со временем растет по мере осаждения частиц. Слой осадка примем как однородную пористую среду. Задачу рассмотрим в одномерной постановке. Параметры жидкой и дисперсной фаз отмечены нижними индексами 1 и 2 соответственно.

Для описания поведения суспензии вне пористого осадка используем систему уравнений одномерного безынерционного движения двухфазной смеси [1]. Скорость фильтрации жидкости определяется по формуле (закон Дарси) [4]

,    .                                                                                         (1)

Здесь Н – гидродинамический напор, C – коэффициент фильтрации, k – проницаемость пористой среды.

Из уравнений движения можно определить отдельно скорости жидкой и дисперсной фаз суспензии

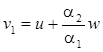,    ,     ,    .                                                                       (2)

Для скорости перемещения поверхности осадка имеем следующую формулу

,                                                                                       (3)

где  – объемная концентрация частиц в осадке.

Используя полученные формулы для скоростей перемещения поверхностей чистой жидкости, суспензии и осадка можно составить уравнения, описывающие изменение положений поверхностей раздела  во времени [5]

,    ,    ,                                                                     (4)

Здесь ,  – характерные времена полного осаждения частиц дисперсной фазы в осадок и фильтрации, причем  (определяются согласно условиям  и  соответственно), T – время полного вытекания жидкой фазы суспензии, включая время истечения жидкости из пористого осадка (устанавливается исходя из условия h=0). Для напора H поставим следующие граничные условия. При этом ввиду достаточно малой скорости движения жидкости давление на поверхности осадка примем равным гидростатическому давлению, а на дне сосуда – равным нулю. С учетом граничных условий распределения скорости фильтрации и давления вдоль осадка запишутся в формах

,    .                                                                           (5)

Важно отметить, что величина H зависит не только от координаты, но и от времени (неявно), поскольку координаты поверхностей раздела, на которых ставятся граничные условия для H, меняются со временем. Нестационарность задачи в этом случае неявно проявляется через граничные условия. При h→ величина скорости фильтрации приближенно равна С. 

С учетом принятых начальных условий из системы (4) следуют два соотношения, связывающие координаты поверхностей раздела

,      ,                                                                                  (6)

,     ,     ,

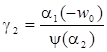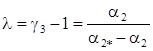где ,  – высота суспензии и толщина осадка в начальный момент времени. Таким образом, задача сводится к определению закона изменения координаты одной из поверхностей раздела, например, поверхности чистой жидкости h (положения остальных поверхностей определяются исходя из (6)). Из второго соотношения (6) нетрудно получить формулу для толщины осадка, образуемого после полного осаждения дисперсной фазы (когда )

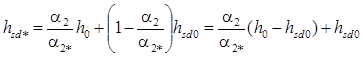.                                                                        (7)

Соотношения (6) также позволяют определить координату поверхности чистой жидкости в момент полного осаждения частиц в осадок

.                                                                                              (8)

Полученные соотношения можно использовать для экспериментального определения значения коэффициента , для этого достаточно только одного измерения высоты чистой жидкости над суспензией в некоторый, вообще говоря, произвольный момент времени . Зная экспериментальное значение коэффициента  можно вычислить объемную концентрацию дисперсной фазы в изучаемой суспензии  при известном значении скорости осаждения одиночной частицы  (или величину скорости осаждения  при известном значении ).

В случае отсутствия фильтрации (С=0) соотношения (6) примут вид

,    ,    .                                                                      (9)

Видно, что в этом случае координаты поверхностей раздела между чистой жидкостью, суспензией и осадком меняются в зависимости от времени по линейному закону. При этом формула для времени полного осаждения частиц  (когда ) имеет вид

,                                                       (10)

или в безразмерных величинах

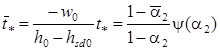.                                                                             (11)

Видно, что при →0 время →1, т.е. стремится к времени осаждения одиночной частицы в чистой жидкости, а при → имеем →0. Отметим, что сомножитель  в (10) отвечает уменьшению времени осаждения дисперсной фазы из-за эффекта повышения высоты осадка (за счет накопления седиментирующих частиц), а величина  в знаменателе ответственна за тормозящее влияние движения жидкости вверх на осаждающиеся частицы.

В случае = имеем , , а уравнение для h примет вид

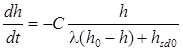.                                                                            (12)

Решение этого уравнения можно выразить в неявной форме

,                                                                                (13)

,    ,     ,     

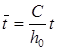
Время полного истечения суспензии через слой осадка (когда ) в этом случае определяется как

,                                                          (14) 

.

Из (14) можно получить несколько приближенных формул. Например, когда начальная высота осадка достаточно мала (), и им можно пренебречь из (14) получим следующую приближенную формулу

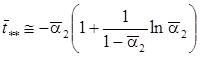.                                                                               (15)

Зависимость (15) ведет себя немонотонно. Максимальное значение, равное она принимает при значении объемной концентрации частиц в суспензии .  

Анализ зависимости (), вытекающей из (14) при фиксированном  показал, что она меняется немонотонно и проходит через максимум, причем

.                                                                                (16)

В целом, формула для общего времени фильтрации суспензии, в течение которого поверхность жидкости из-за фильтрации достигает верхней границы осадка (т.е. выполнится условие  ) имеет вид

.                                          (17)

Полученная формула позволяет вычислить время полной фильтрации суспензии  через время полного осаждения дисперсной фазы  (или через величину ).