Применение теории нечетких множеств для выбора оптимальной модели управления запасами лекарственных средств аптечной сети

Управление запасами лекарственных средств аптечной сети является сложным процессом не только из-за наличия законодательных требований к обязательному ассортименту, контроля величины торговой наценки и широкой номенклатуры лекарственных средств. [1]

Дополнительная сложность управления запасами выражается в том, что каждый аптечный пункт сети функционирует при различных условий снабжения и сбыта.

Зачастую аптеки одной сети снабжаются с одного склада. Распределенность сети приводит к тому, что на аптеки могут накладываться различные ограничения на период поставки, минимальный и максимальный размер заказа. Также варьируется и стоимость доставки. Данные ограничения могут быть в разной степени критичны для пунктов.

В зависимости от сложившихся на локальном рынке аптечного учреждения спроса, условий работы с поставщиками товаров, а также с учетом возможностей финансирования процесса закупки товаров аптечное предприятие должно найти свои собственные ответы на вопросы: насколько большой должен быть товарный запас? Как часто следует закупать товар? Каков должен быть объем одного заказа продукции у поставщика?

Спрос на лекарственный средства будет зависить не только от непосредственной близости других аптек, но и, например, поликлиники, женской консультации, которые влияют на посещаемость. Также учитывается фактор сезонности спроса (например, повышенный спрос у населения в осенне-зимнее время на противопростудные препараты, препараты для профилактики и лечения гриппа, лекарства для повышения иммунитета) и т.д.

Именно поэтому целесообразно выбирать модель управления запасами с учетом особенностей аптеки и условия применения модели. Для этого необходимо проанализировать наиболее используемые для аптечного предприятия модели формирования товарных запасов, а также их применимость при различных условиях снабжения и сбыта.

Существуют две базовые модели (стратегии) формирования товарных запасов для аптечного предприятия:

1. Модель с фиксированным объемом заказа;

2. Модель с фиксированным интервалом времени между заказами. [2]

К наиболее распространенным модификациям основных динамических моделей управления запасами относят:

1. Модель с установленной периодичностью пополнения запасов до постоянного уровня;
2. Модель «минимум—максимум».

Каждая из приведенных моделей имеет как свои преимущества, так и свои недостатки:

Таблица 1.

Особенности наиболее используемых моделей управления запасами

На основании приведенного описания можно выделить параметры, которые будут оказывать влияние на выбор модели управления запасами:

х₁ – оборачиваемость (раз/мес)

х₂ – стоимость хранения и содержания запасов (тыс. руб)

х₃ – оценка характера динамики спроса (-)

х₄ – ограничения на периодичность выполнения заказов (дн)

х₅ – ограничения на минимальный размер заказа (кг)

х₆ – ограничения на грузоподъемность поставщика (кг)

Перечисленные параметры определяются специалистом отдела управления запасами на основании данных снабжения и сбыта.

Будем определять оптимальную модель управления запасами из приведенного набора моделей:

d₁ – двухуровневая модель («минимум – максимум»);

d₂ – модель с фиксированным размером запаса;

d₃ – модель с установленной периодичностью пополнения запасов до постоянного уровня;

d₄ – модель с фиксированным интервалом времени между поставками;

Введем следующие лингвистические переменные (рис.1):

D – коэффициент сложности управления запасами, который определяет модель из набора d_1÷ d_4;

y – переменная хранения и расходования запасов, которая зависит от параметров { х_1, х₂}

z - переменная ограничений поставщика, которая зависит от параметров { х_4, х_5, х₆}

Структура модели для выбора оптимальной модели управления запасами показана на рис. 1 в виде дерева логического вывода, отвечающего соотношениям:

D = f_d (y, x₃, z)                                                                                                                    (1)

y = f_y (x₁, x₂)                                                                                                                      (2)

z = f_z (x₄, x₅, x₆)                                                                                                                   (3)

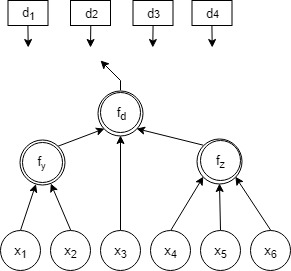
Рисунок. 1. Дерево логического вывода

Для решения задачи выбора модели специалисту отдела управления запасами необходимо определить диапазон значений параметров, а также сформировать базу знаний.

Для оценки параметров х₁, х₂, х₄, х₅, х₆ используется терм-множество:

L₁={низкий (Н), ниже среднего (нС), средний (С), выше среднего (вС), высокий (В)}.

Для оценки параметра х₃ используется терм-множество:

L₂={стабильный (С), слабо колеблется (слК), колеблется (К), сильно колеблется (сК)}.

Для осуществления расчетов целесообразно использовать программное средство MatLab, предусматривающий специализированный инструмент FuzzyLogic.

Внедрение данной методики предполагает повышение качества организации деятельности по управлению запасами, так как она подразумевает индивидуальный подход к формированию запасов каждого аптечного пункта, а также позволяет адаптироваться к изменению параметров снабжения и сбыта.